最新の予測はブログ「新型コロナウィルス感染症収束予測を検証中(アップデート中)」をご覧ください。毎週月曜日にアップデートしています。
2020年4月16日付のブログ「外出自粛は新型コロナ・ウィルス感染症の収束を速めるか?」と2020年11月22日付ブログ「新型コロナ・ウィルス感染者数が波打つ理由」で解析した複数合成波で今後の感染者数を予測しています。図1の青色のドットは厚生労働省のホームページで公表されている国内感染者数を週別に集計したものです。青色の実線は2021年12月までの各変異種の合成波です。
2021年12月の後半に入り、漸減傾向にあった感染者数は増加に転じる兆候が見受けられました。海外では変異種であるオミクロン株に感染するひとが急増し、日本にもその影響が波及しつつあった2021年1月2日に今後の感染者数の予測を以下のふたつのシナリオで行いました。
シナリオ a :これまでの変異種の平均的な感染力とする場合 → オレンジの破線
シナリオ b:これまでに最も感染力が強かった第11種と同等とする場合 → グレーの破線
変異種の出現に関する数理的考察は、2021年8月18日付のブログ「新型コロナウィルス変異種の存在を説明する数理モデル – 逃げる抗原、追いかける抗体」をご覧ください。
図1
新型コロナ・ウィルスの感染者数(単位:千人)
破線が各変異種の感染者数、実線が合成波
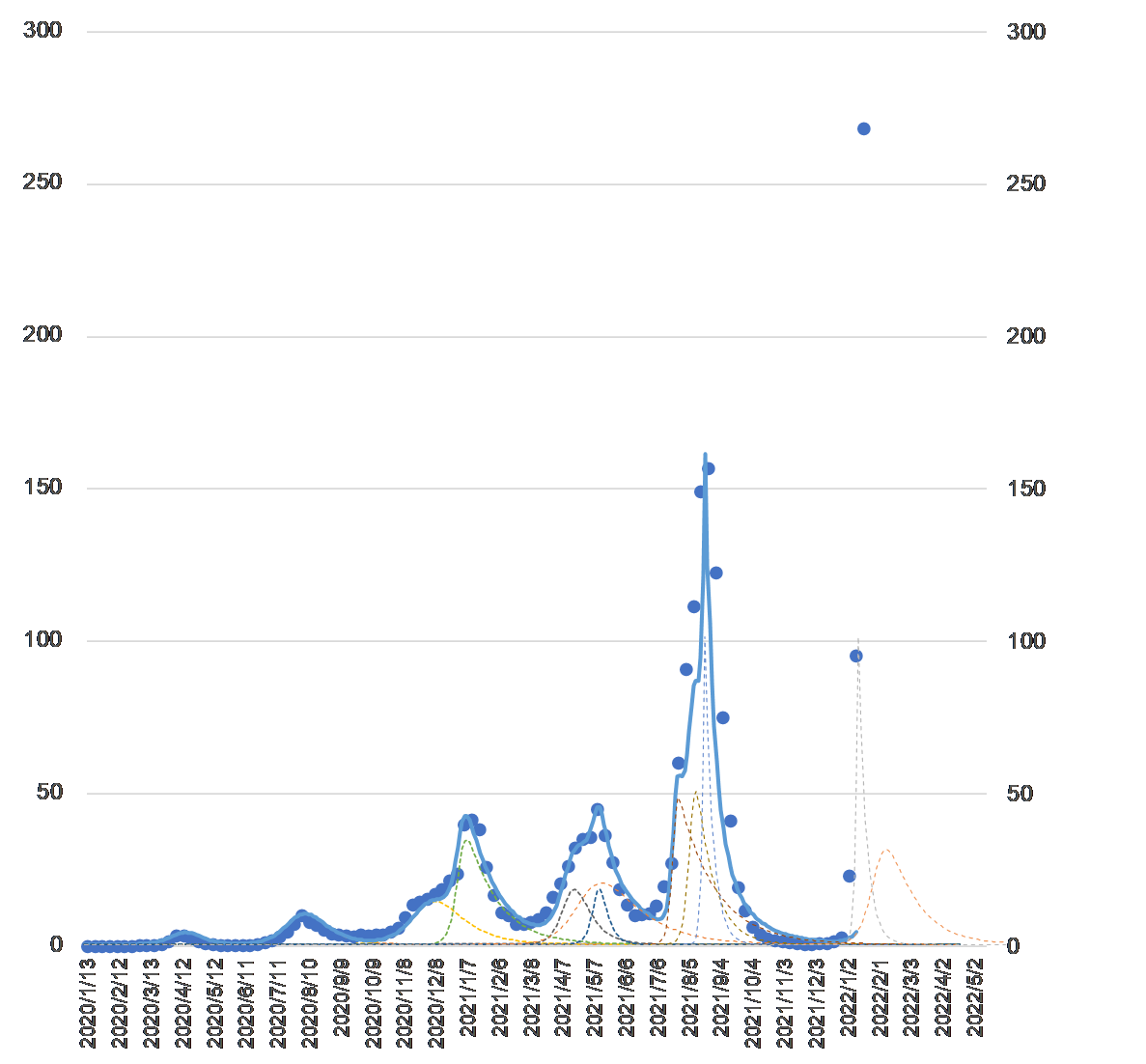
2022年1月23日現在
最新のデータに基づき予測を修正します。
<収束予測を計算するための数理論>
感染する可能性のある人の数を $x$(以下、未感染者)、感染していて他人にうつす可能性のある人の数を $y$(以下、感染者)としたときに、それぞれの変化率は以下の微分方程式に従うとして予測しています。(注意:「未感染者」には、感染者との接触を避けている、感染しないようにしている、ひとは含まれません。詳しくは 2020年4月16日付ブログ「外出自粛は新型コロナ・ウィルス感染症の収束を速めるか?」と2020年11月22日付ブログ「新型コロナ・ウィルス感染者数が波打つ理由」をご覧ください。)
$$\frac{dx}{dt}=-bxy\tag{1}$$
$$\frac{dy}{dt}=bxy-cy\tag{2}$$
式 $(1)$ は未感染者が感染者と接触して減少すること、式 $(2)$ は、その結果感染者数が増加する一方で、治癒したり、亡くなったりして感染者ではなくなること、を表しています。係数の $b$ は「感染係数」、$c$ は「治癒係数」です。合成波(青色の実線)を構成する各波(破線)の係数は以下のとおりです。
表1

図2
新型コロナ・ウィルスの感染者数(単位:千人)
破線が各変異種の感染者数、実線が合成波
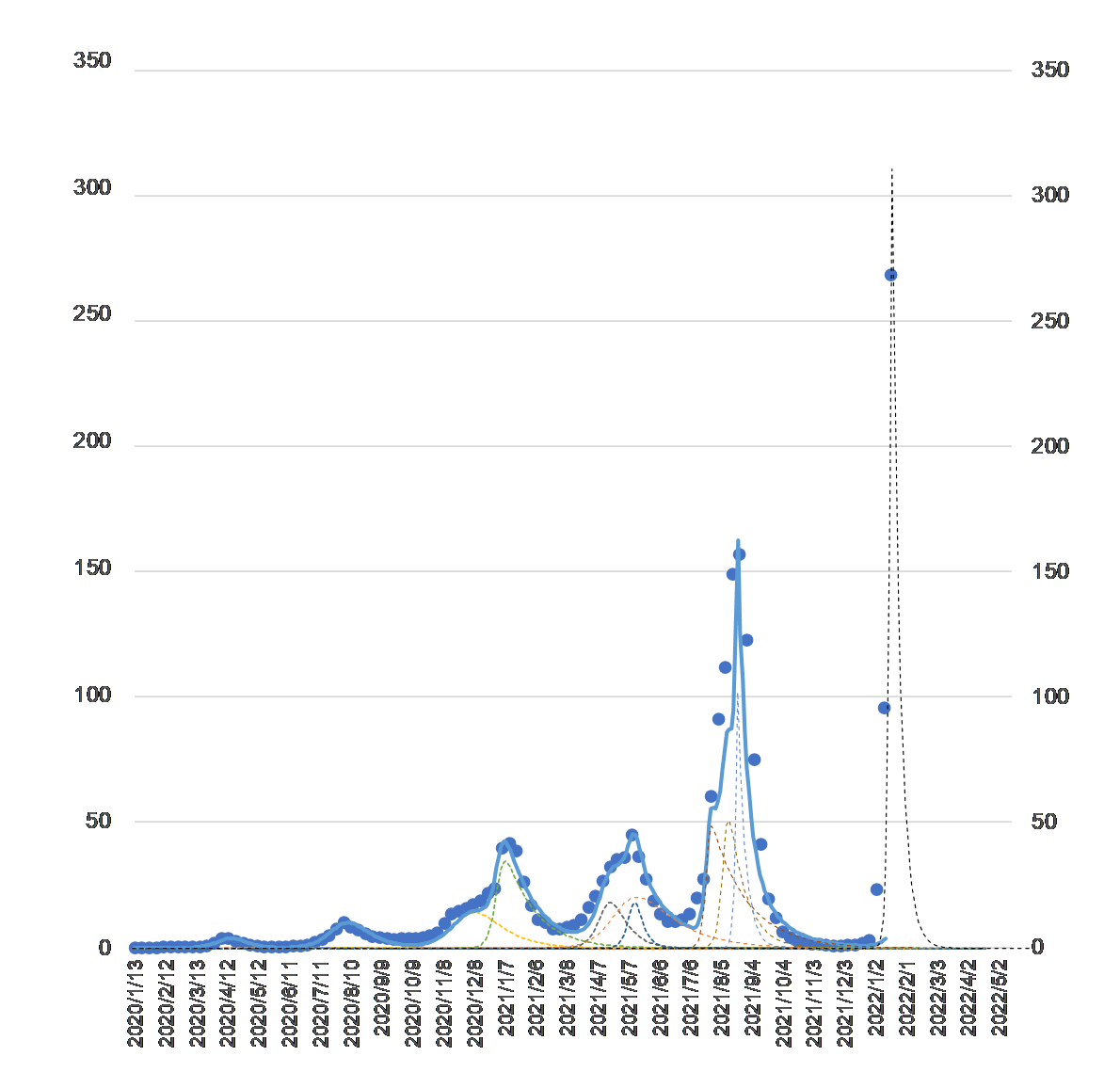
表1のシナリオ C にもとづく収束予測(2022年1月23日現在)
以下は、厚労省ホームページ、報道関連資料から集計しグラフ化したものです。ご参考まで。
図3
PCR検査数、陽性者数、死亡者数の累計(対数軸)
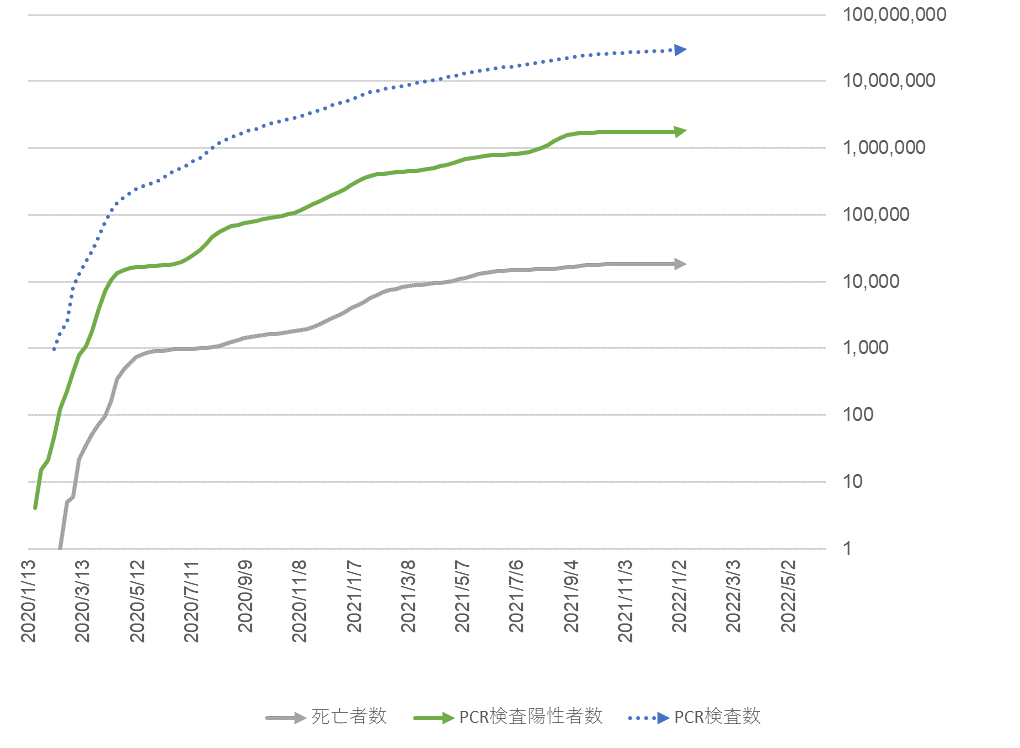
2022年1月23日現在
図4
PCR検査陽性率と陽性者死亡率の週別推移
(2020年8月3日の週~2022年1月24日の週)
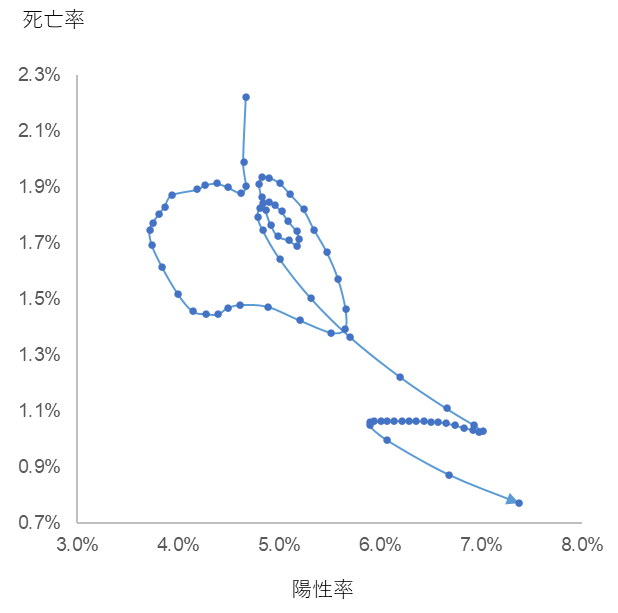
陽性率が上がる一方で、死亡率は下がる傾向にあります。ふたつのデータをエクセルの関数 =CORREL(陽性率の推移,死亡率の推移) に入れて計算すると、相関係数 r = -0.82 が得られ、強い負の相関があることがわかります(一般に相関係数 r が -1.0 ≦ r ≦ 0.7 にあると「強い負の相関」があるとされる)。
図5
新型コロナウイルスによる死亡者数の月別推移
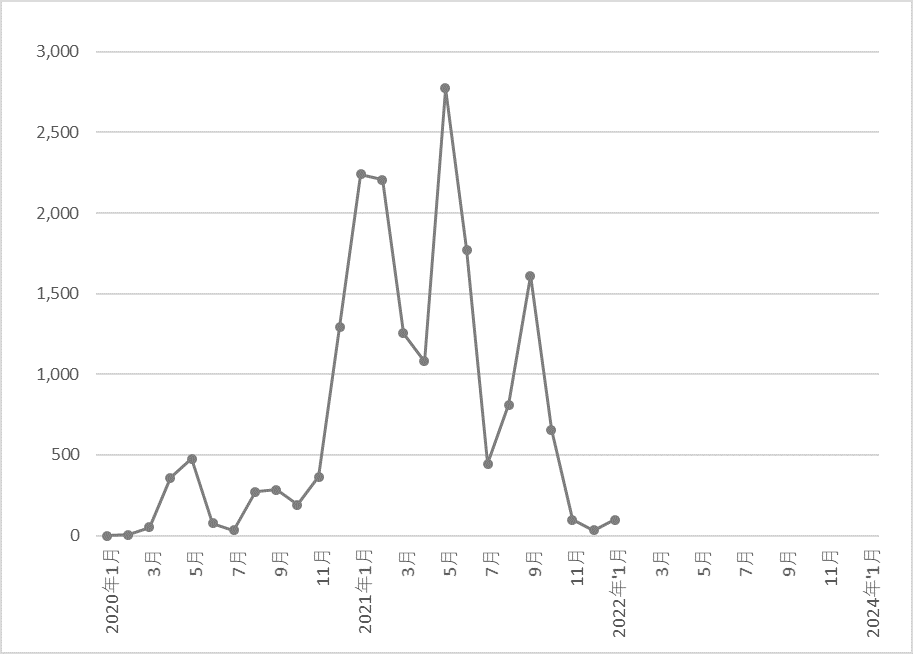
2022年1月現在
<比較資料>
COVID-19(グレー)と100年前に大流行したスペイン風邪(青)の月別死亡者数の比較
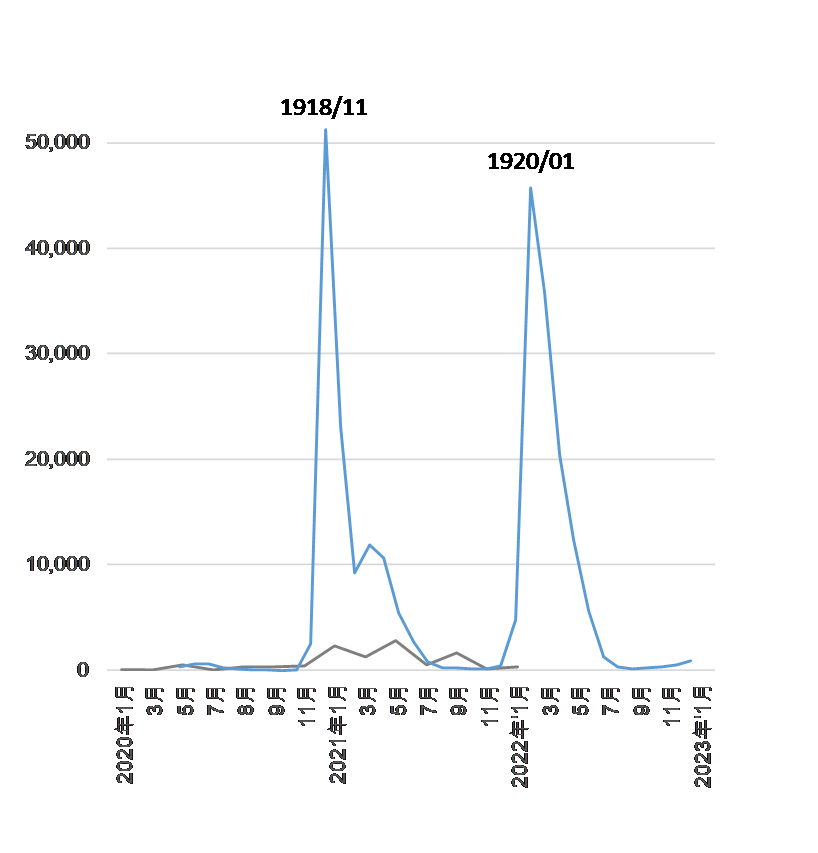
スペイン風邪のデータは東京都健康安全研究センターのHPより。
比較のため横軸と縦軸のスケールを合わせています。
東京都健康安全研究センター 年報56、2005 によると、「スペイン風邪による感染者数は2,380万人、死亡者数39万人」ですので、感染者数で新型コロナウィルス(2022年1月現在)の14倍、死亡者数は21倍です。インフルエンザの特長として「流行時期によりウイルスが変異することが往々にして観測される.スペインかぜ流行の際にも原因ウイルスが変異し,その結果として死亡率が大幅に増加したものと考えることができる.」と述べられており、さらには「今後のインフルエンザ対策を企画立案する際には,「再燃」について十分配慮していくとともに,インフルエンザウイルスの抗原性を経時的に観測していき,ウイルスの変異にすばやく対処することがぜひとも必要である.ウイルス変異を早期に検出できれば,新型インフルエンザの流行を未然に防ぐことも可能になるものと考える.」と、変異とその対応への重要性が指摘されています。
以上
記事一覧へ戻る