スカイダイビングは富士山頂くらいの高さから、地球の重力に引っ張られながら、空気の抵抗を受けて50秒くらいの空中遊泳を楽しむスポーツです。ニュートンは、質量 $m$ に加速度 $\frac{dv}{dt}$ をかけたものが力 $F$ である、といっているので、
$$m\frac{dv}{dt}=F\tag{1}$$
実際、質量 $m$ のダイバーにかかる力 $F$ は重力 $g$と、空気抵抗の $kv^2$ であることがわかっており、後者は重力と反対方向にかかるので、
$$F=mg-kv^2\tag{2}$$
と書けます。よって、$(1)=(2)$ より、
$$m\frac{dv}{dt}=mg-kv^2\tag{3}$$
変形して、
$$\frac{dv}{dt}=g-\frac{k}{m}v^2\tag{4}$$
これで、微分方程式ができましたので、それを積分すれば、任意の時間 $t$ におけるスカイダイバーの速度 $v$ を求める式が得られます。積分の過程は省略させていただいて、結果だけを示すと、
$$v=Vtanh\frac{t}{T}\tag{5}$$
が得られます。ここで、$V=\sqrt{\frac{mg}{k}}$、$T=\sqrt{\frac{m}{gk}}$、です。
$tanh$ は、見慣れないですが、「タンジェント・ハイパボリック」と読みます。具体的には、
$$tanhx=\frac{e^x-e^{-x}}{e^x+e^{-x}}\tag{6}$$
で、指数関数の分数式をひとまとめにしたものです。
式 $(5)$ を用いて、上空 $3,800m$ からスカイダイビングしたときの様子をグラフにすると、図1のようになります。
図1
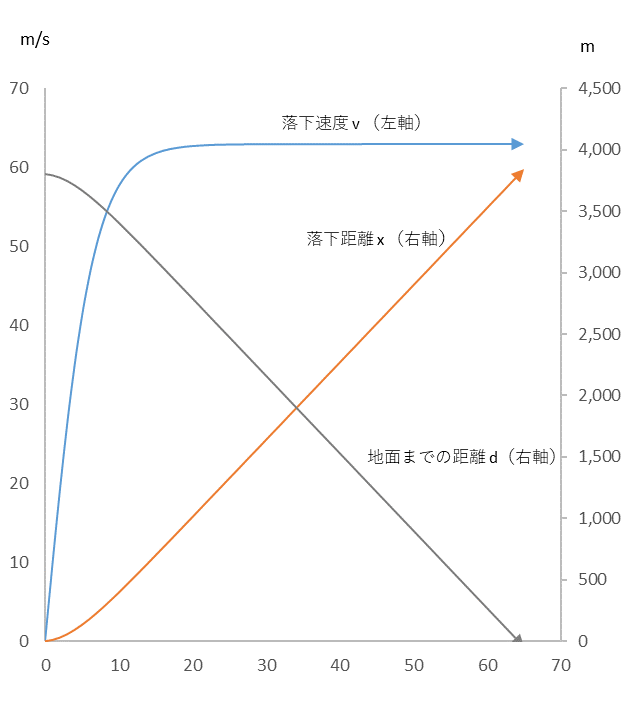
上空 3,800m から、スカイダイビングするとき、その後の落下速度は、
微分方程式 $\frac{dv}{dt}=g-\frac{k}{m}v^2$に支配される。
g=9.8m/s2、k=0.25kg/m、m=100kg、として計算した図。
落下速度 $v$ は徐々に速くなり、20秒くらいで 63m/s に達しますが、興味深いことに、その後はそのまま等速運動を続けます。パラシュートを開く50秒後の高度はおよそ900mですが、もし、ここで何らかの理由でパラシュートが開かなくても、あせらず十秒以内になんとかすれば地面に激突せずにすみます。
ここで、わたしが最も注目するのは、微分方程式に質量 $m$ が含まれる、つまり、「重い方が早く落ちる」という事実です。
$$\frac{dv}{dt}=g-\frac{k}{m}v^2\tag{4}$$
「ガリレオによるピサの斜塔実験(大小の金属玉を落として、落下速度が質量に影響されないことを証明してみせた)」はあまりに有名です。実際、50m くらいの高さですと二個の金属玉は一秒もしないうちに地面に落ちてしまうので、見た目、ほぼ同時だったのでしょう。
さて、本日の本題はここからです。
図1の落下距離 $x$ (オレンジ色の線)に注目してください。落ちはじめの10秒くらいは曲線ですが、その後はほぼ右肩上がりの直線です。唐突ですが、私には、それが企業の成長にみえてしまいます。2021年5月6日付のブログ「数理経営のすすめ」で、いろいろな成長パターンをご紹介しましたが、本日は、そのときに気付いていなかった新たな成長パターン「スカイダイビング型成長」について考えます。
「成長」を「落下」に例えることに違和感がある方は、スカイダイバーではなく、自ら上昇することができるロケットを想像してください。地球の重力 $g$ に相当するのが、ロケットの推進力 $a$ です。そのどちらも空気抵抗 $kv^2$ を受けながら、移動距離 $x$ を伸ばしていきます。その距離 $x$ があなたが今手掛けている事業の売上だと思ってください。質量 $m$ は事業の規模、空気抵抗係数の $k$ は、逆風となる環境や、他社との競争と捉えます。
まずは、推進力の $a$、規模の $m$、環境・競争の $k$ の三つ係数に対する、売上 $x$ の感度をチェックしましょう。
図2
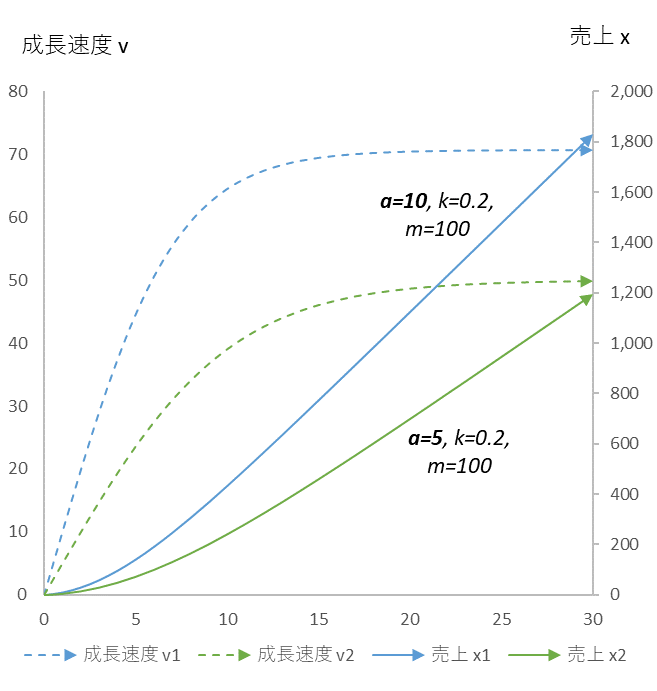
推進力係数 $a$ だけを変化させたときの成長速度 $v$ と売上 $x$ の推移
推進力係数 $a$ が半分になると、売上は 35% 減少
図3
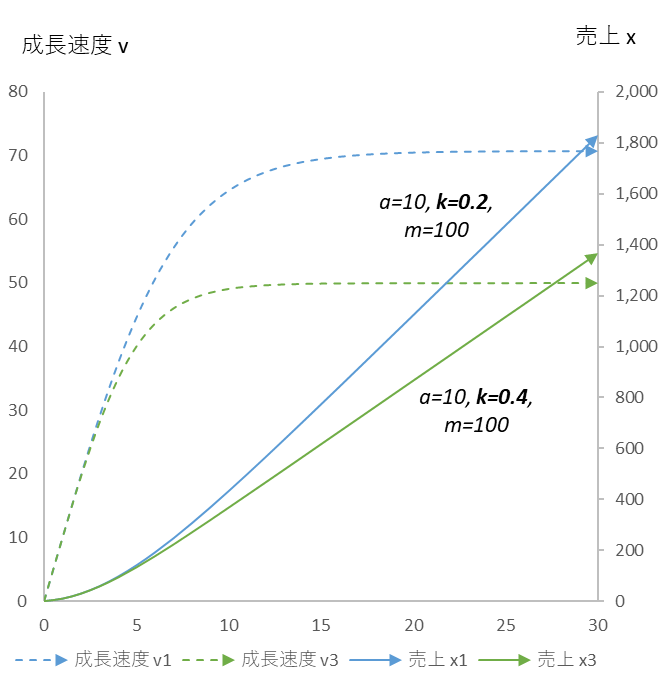
環境競争力係数 $k$ だけを変化させたときの成長速度 $v$ と売上 $x$ の推移
環境競争力係数 $k$ を 50% 増(0.2→0,4) にすると、売上は 25% 減少
図4
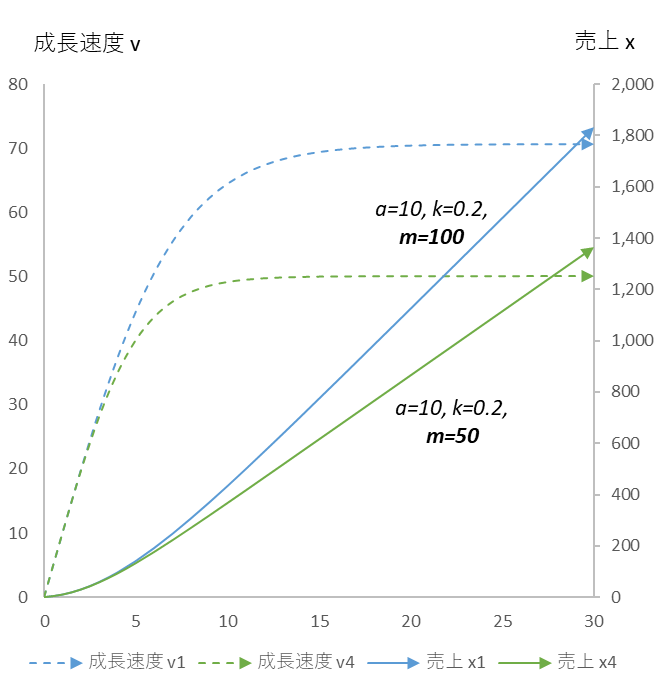
規模係数 $m$ だけを変化させたときの成長速度 $v$ と売上 $x$ の推移
規模係数 $m$ を 50%減(100→50)にすると、売上は 25% 減少
三つの係数のうち、とくに環境競争係数 $k$ はランダムに変化することが予想されますので、$k$ に 乱数を掛け合わせてゆらしてみましょう。
図5
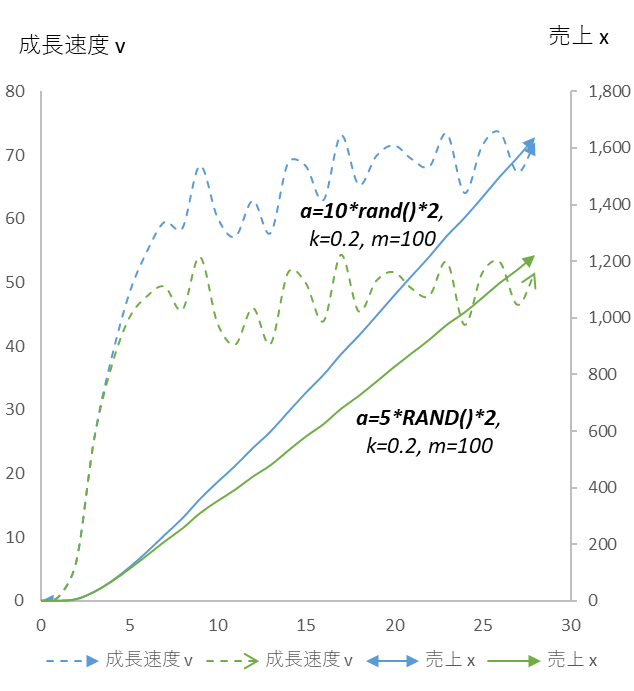
環境競争係数 k にゆらぎ(=RAND()*2)を与えると、売上 x は約10%減少、
さらに、k を 50% 増(0.2→0.4)にすると、売上は 約25% 減少。
では、ここで実際の企業の売上を予測してみます。2021年5月6日付けブログでも紹介したセブンイレブンの過去47年間(昭和49年度~令和3年度)の売上推移にフィットするよう、三つの係数、$a$, $k$, $m$ を選びます。図6をご覧ください。
図6
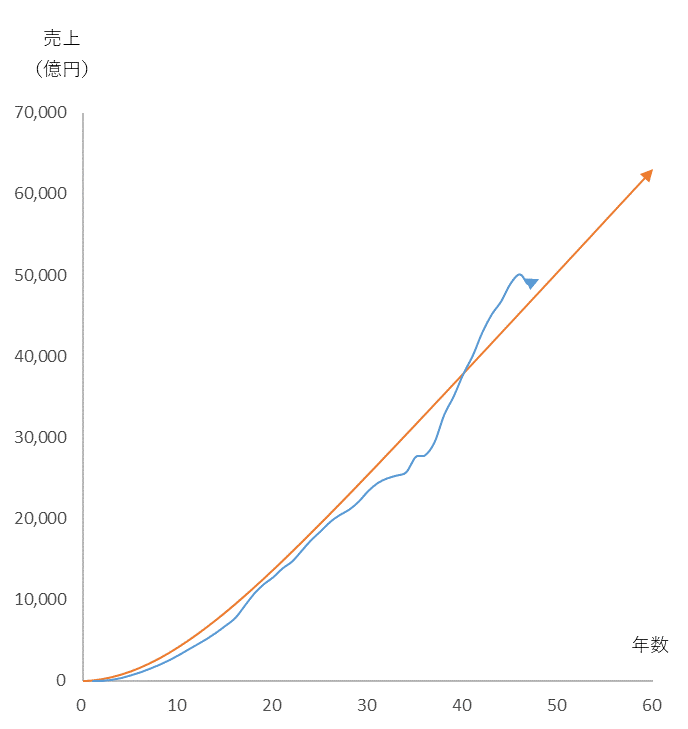
セブンイレブンの売上未来予測図
式 (4) において、推進力係数 $a$=80、環境競争係数 k=0.05、規模係数 m=1,000として令和16年度(2034年度)の売上を予測した。
セブンイレブンは令和16年度(2034年度)に還暦を迎えますが、そのとき、売上は6兆3千億円前後に達していることが予測されます。一方、2021年5月6日付けブログの予測($\frac{dx}{dt}=at+b$)は、売上予測曲線が時間の二次関数となっているため、還暦売上は8兆2千億円と、かなり大きく出ていました(図7)。スカイダイビング型予測(図6)の方が1兆9千億円低いことになります。
図7
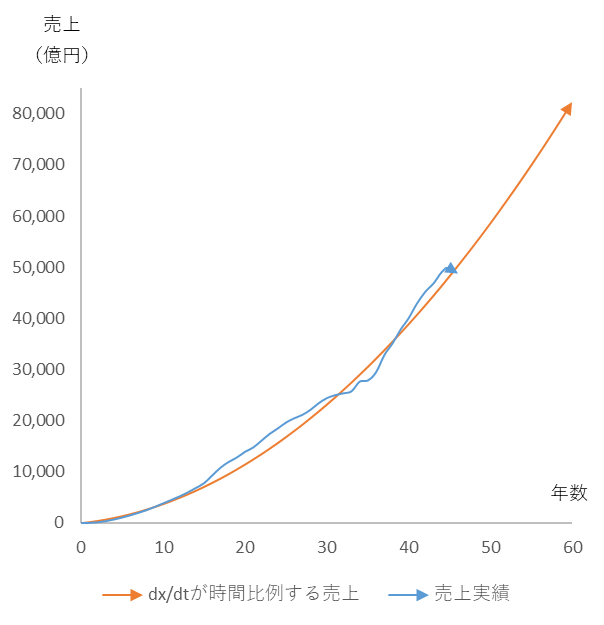
$\frac{dx}{dt}=at+b$ において、$a$=40、b=150 の売上予測(二次関数曲線)
(2021年5月6日付けブログ、数理経営のすすめ その1「成長」より)
下図は業界二位のローソンとの比較です。実線が売上実績、破線が微分方程式 $(4)$ による売上予測です。
図8
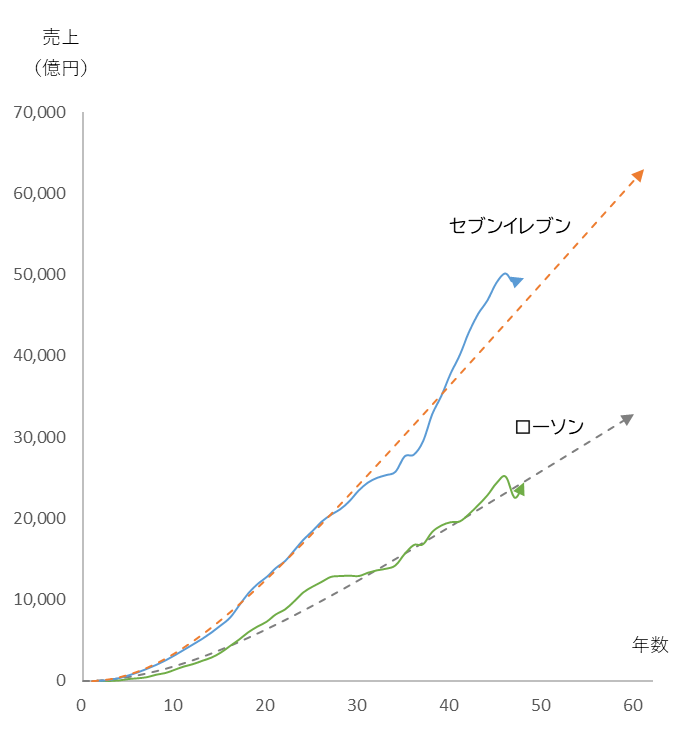
セブンイレブン:推進力係数 $a$=80、環境競争係数 k=0.05、規模係数 m=1,000、12年後の売上予測 6.3 兆円
ローソン:推進力係数 $a$=35、環境競争係数 k=0.05、規模係数 m=700、12年後の売上予測 3.2 兆円
ローソンの売上高は 同社公式サイトのグラフ から読み取りました。
両社の公式サイトによると、2022年現在、セブンイレブンの店舗数は21,327店、ローソンは14,656店、ですので、単純に店舗数だけで比較するとローソンはセブンイレブンのほぼ七割の規模ですが、売上高でローソンがセブンイレブンの五割くらいに留まっているのは、推進力係数の差によるものと思われます。この係数が変わらない限り、売上高比率もずっと「二対一」のまま、ということになります。
おわり
記事一覧へ戻る