2021年5月6日付のブログ でいろいろな成長のパターンを計算する方法をご紹介しましたが、その中に「Ｓ字カーブ成長」がありました。成長率が時間経過とともに、小→大→小と変化する成長です。売上を $x$、時間を $t$、成長の上限を $K$ としたとき、このS字カーブ成長は以下の数式で表されます。

$$\frac{dx}{dt}=rx(1-\frac{x}{K})\tag{1}$$

$$x_{t}=\frac{K}{1+(\frac{K}{x_{0}}-1)e^{-rt}}\tag{2}$$   

式 $(1)$ が微分方程式、式 $(2)$はその解で、それを使って計算した成長の時間経過が図１です。このS字カーブは一般にロジスティック曲線（成長）と呼ばれています。

図１

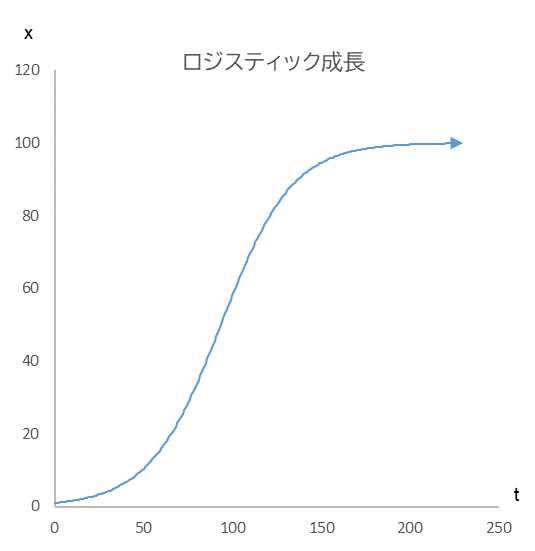
x₀=1.0, r=0.05, K=100 のときのロジスティック成長

 

ではここで具体的な事例をみましょう。図２は自動車検査登録情報協会から発表されている日本のエコカー（ハイブリッド車＋電気自動車）の保有台数の推移です。

図２

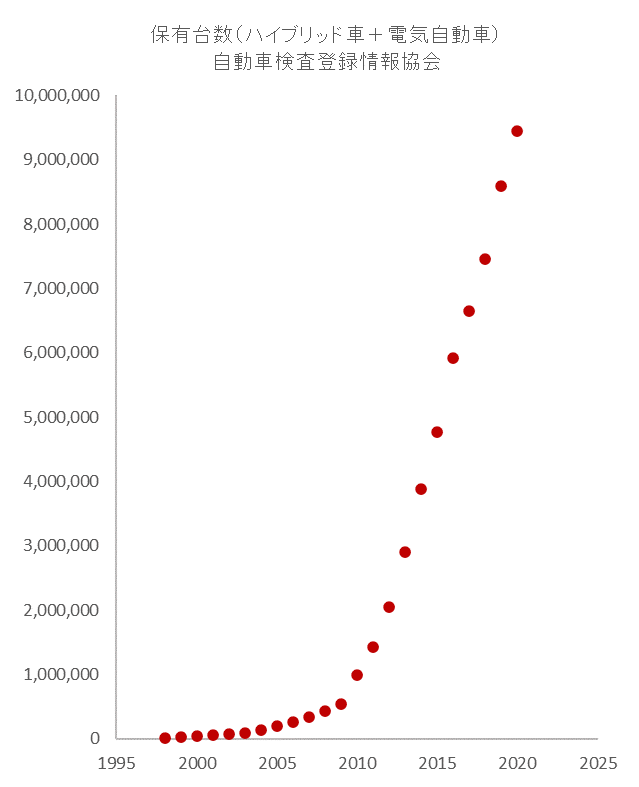
図１と比較するとおおよそ下半分が経過したようにもみえますので、ここにロジスティック曲線を重ね合わせます（図３）。

図３

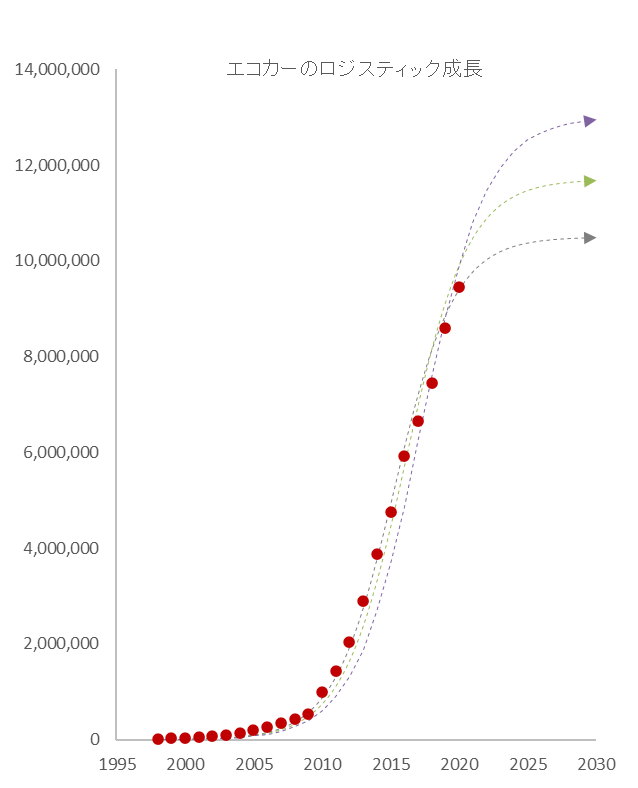
x₀=4,066台（1998年）, r=0.455, 0.440, 0.420, K=10.5百万台、11.7百万台、13.0百万台 のときのロジスティック成長

 

三通りのロジスティック曲線を書き込みました。式 $(2)$ は、初期値（x₀）、成長率（r）、環境容量（K）から構成されます。これらは予め決めておく必要があるのですが、注意すべきは環境容量の $K$ です。上限を予め決めておく必要があるならもはやそれは成長予測とはいえません。

そこで、成長の予測モデルをロジスティック型からロケット型に（ 2022年9月24日付ブログ）に変更してみましょう。ロケット型はその推進力が途絶えな限り飛び続けるのが特長です。

ニュートンは、質量 $m$ に加速度 $\frac{dv}{dt}$ をかけたものが力 $F$ である、といっているので、

$$m\frac{dv}{dt}=F\tag{3}$$

質量 $m$ 、速度 $v$ のロケットにかかる力 $F$ は加速度 $a$と、空気抵抗の $kv^2$ であることがわかっており、後者は推進力と反対方向にかかるので、

$$F=ma-kv^2\tag{4}$$

と書けます。よって、$(3)=(4)$ より、

$$m\frac{dv}{dt}=ma-kv^2\tag{5}$$

変形して、

$$\frac{dv}{dt}=a-\frac{k}{m}v^2\tag{6}$$

ここで、ロケットを事業に置き換えると、$a$ は事業の加速度、$m$ は事業規模、$kv^2$ は成長を抑制する事業環境と捉えることができます。つまり、式 $(6)$ は事業の実質加速度を示していることになりますので、ここから単位時間 $t$ の成長を計算することができます。 では、さっそく図２にロケット成長線を書き込んでみましょう（図４）。

図４

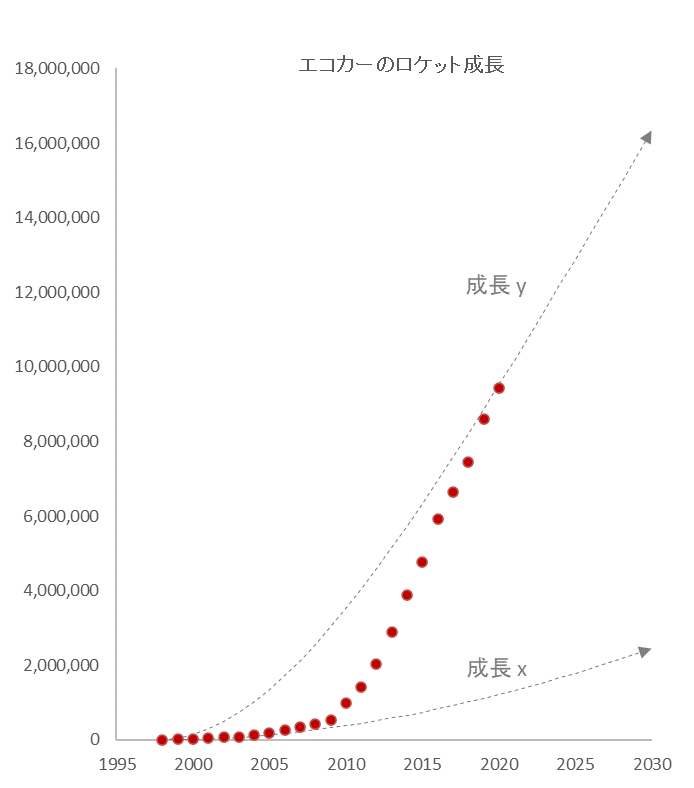
成長ｘ：　a=5,000, k=0.01, m=100,000

成長ｙ：　a=50,000, k=0.01, m=100,000

 

成長ｘと成長ｙの違いは加速度 $a$ の違いのみでその他の条件は同じです。それぞれの成長曲線を実績（赤色のドット）と比較すると、2007年ごろまでは成長 x の曲線に、その後は成長 y の曲線に近いようですので、両方を足し合わせてみましょう（図５）。

図５

成長x+ y：　a=5,000（1998～2007）, a=50,000（2008～）k=0.01, m=100,000

 

二段ロケットにすることで過去の成長推移を見事にトレースすることができました。

ところで、式 $(6)$ は速度 $v$ の時間微分ですので、これを時間 $t$ で積分すれば速度 $v$ の関数 $v(t)$ を求めることができます。途中の計算を飛ばして結果だけを示すと、

$$v(t)=Vtanh\frac{t}{T}\tag{7}$$

となります。ここで、$V=\sqrt{\frac{ma}{k}}$、$T=\sqrt{\frac{m}{ak}}$ です。

ちなみに、 式 $(6)$ は速度の変化率ですから、これがゼロになったときに速度変化が止まり、等速で進みます。

$$\frac{dv}{dt}=a-\frac{k}{m}v^2=0\tag{8}$$

変形すると、$v=\sqrt{\frac{ma}{k}}$ となり、これがまさに式 $(7)$ における $V$ です。 一方、$tanh\frac{t}{T}$ は時間経過とともに 1.0 に漸近する性質がありますので、結局 $v(t)$ は $V$ に収束します。

成長 x と成長 Y の到達速度 $V$ を計算してみると、それぞれ

成長 x の到達速度 V_x = 223,607

成長 y の到達速度 V_y = 1,072,381

成長 x + y の到達速度 V_x+y = 1,295,987 

つまり、エコカーの年間増加数の上限はおよそ1.3百万台であることが分かります。ちなみに、2024年時点での年間増加数は1.1百万台で、エコカーの保有数は14百万台です。四輪車の総保有数をおよそ80百万台とすると普及率は14%です。10年後の2034年のエコカーの保有率は図５よりおよそ26百万台。人口減も鑑み、四輪車の総保有数は80百万台で横ばい、と仮定すれば、10年後のエコカーの普及率は三割を超えますが、その前に三段目のロケットが噴射してさらに普及が加速する可能性もありそうです。

おわり

 

 

記事一覧へ戻る