2023年4月15日付のブログ(未来の売り上げを確率的に予測する)で「三本の矢」をご紹介しました。
1)現状維持を示す線(基準線)
2)平均的な成長を示す線(μ)
3)拡散範囲を示す線(±v)
スタート地点(初期値)を 1.0 とすれば上記のみっつはそれぞれ時間 $t$ の関数として、
$$x_{t}=1.0\tag{1}$$
$$x_{t}=x_{0}e^{(r-\frac{v^2}{2})t}\tag{2}$$
$$x_{t}=x_{0}e^{(r-\frac{v^2}{2})t+v\sqrt{t}}\tag{3}$$
で表すことができます。では、具体例をご紹介しましょう。
まずは世界の代表的な株価指数を採り上げます。株価指数は各国の経済状態のバロメーターですからその明暗がどう分かれているのか気になるところです。図1は2021年1月から2023年12月までの日本を含む八地域の株価の推移です。それらの平均である太い青線がオレンジの $μ$線(中央値)に絡みついているのがわかります。
明暗の範囲が $±v$線で表されており、時間の経過とともに八つの指数の拡散幅が大きくなっているのがわかります。基準線の $1.0$ より上側がプラス成長、下側がマイナス成長です。2021年1月から三年が経過して、日本、インド、欧米はプラス成長、中国(上海と香港)がマイナス成長です。中国経済の減速は気になる点ではありますが、私がより注目するのは「三本の矢」がこれらの「明暗」をあらかじめ予測している、という点です。あらゆる事象は確率的に成長し、その結果として明暗が分かれます。
図1
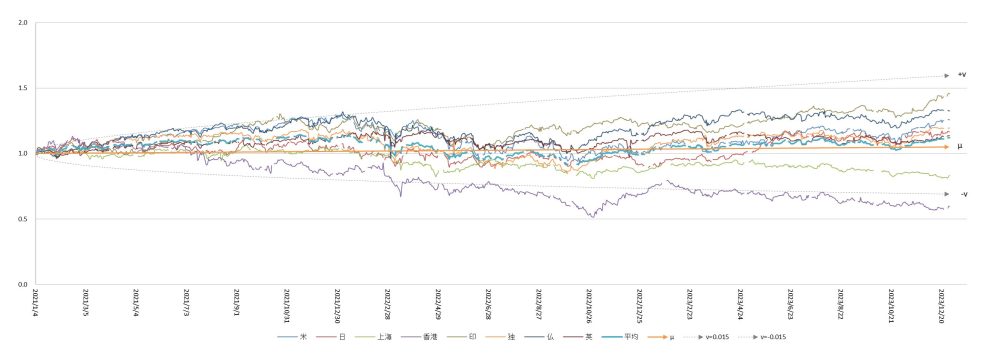
2021~2023年 世界の株価指数の推移(x0=1.0, r=0.000176, v=0.015)
「データの平均とばらつき」の解析は正規分布で行えますから、実際のデータ(表1)から算出した正規分布図を図1に重ね合わせてみましょう(図2の破線)。平均が徐々に上方へ移動するとともに、データが拡散しているのがわかります。
図2
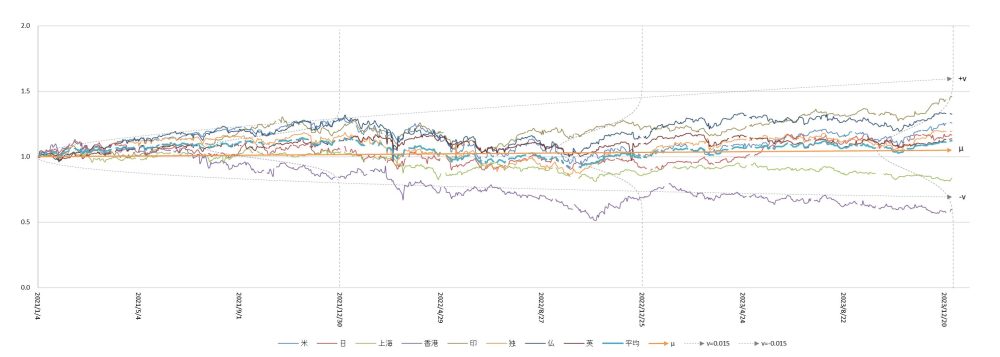
2021~2023年 世界の株価指数の推移と正規分布図(x0=1.0, r=0.000176, v=0.015)
表1
| 2021年 | 2021~2022年 | 2021~2023年 | |
| 最大値 | 1.304 | 1.320 | 1.460 |
| 最小値 | 0.828 | 0.515 | 0.515 |
| 平均 | 1.082 | 1.049 | 1.056 |
| 標準偏差 | 0.086 | 0.136 | 0.155 |
では、次に私が日々フォローしている日本企業(五社)の株価の推移をチェックしてみましょう。ちなみに、五社の選定基準は、異業種である、業界のトップクラスである、常日頃お世話になっている、の三点です。
図3
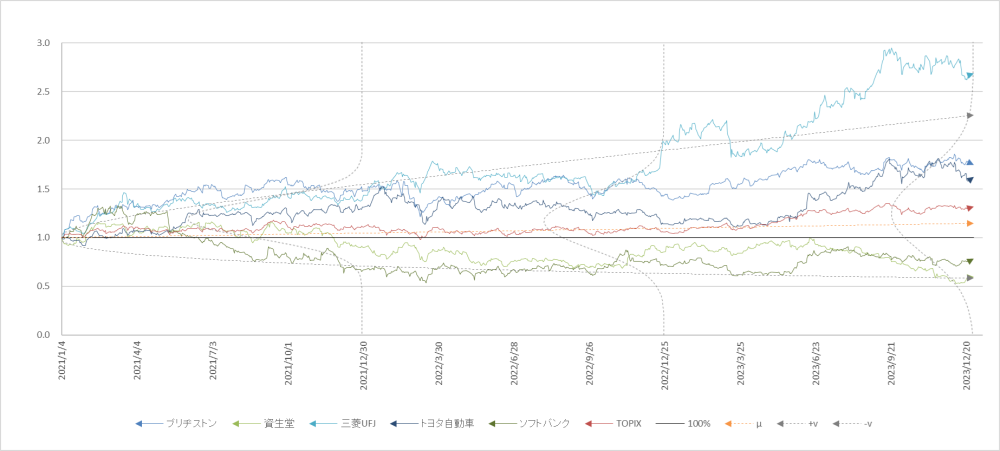
2021~2023年 日本企業五社の株価推移と正規分布図(x0=1.0, r=0.0005, v=0.025)
表2
| 2021年 | 2021~2022年 | 2021~2023年 | |
| 最大値 | 1.6207 | 1.9911 | 2.9512 |
| 最小値 | 0.6372 | 0.5325 | 0.5306 |
| 平均 | 1.1703 | 1.1669 | 1.2354 |
| 標準偏差 | 0.1952 | 0.2845 | 0.4172 |
ここでも世界の株価指数と同様のことが観察されます。注目すべきは、TOPIXが $μ$線に絡みながら成長していること、データの拡散があらかじめ想定した $±v$線内で行われること、 つまり事象が数理論にもとづく「三本の矢」に沿って成長するという点です。図3にもしTOPIXの全銘柄の推移を書き込めば、 $±v$線内の領域はびっしりと塗りつくされることでしょう。
図2、図3ともに 2021/1/4 の終値を初期値にしていますが、初期値をどこにとっても同じ現象が観察されます。株価が経済状態のバロメーターであるとすれば、世界中の経済は数式(2)と(3)に支配されていると言っても過言ではありません。そして、その数式に「初期値 $x_{0}$、基本成長率 $r$、ゆらぎ係数 $v$ 」のわずかみっつのパラメーターしかないことに、万物の真理が潜んでいるように思えてなりません。
つづく
記事一覧へ戻る