突然ですが、図1は2021年1月4日の八か国の 主要株価指数 終値を $1.0$ に揃えて、 2022年12月30日までの同指数の日次終値をグラフ化したものです。
図1
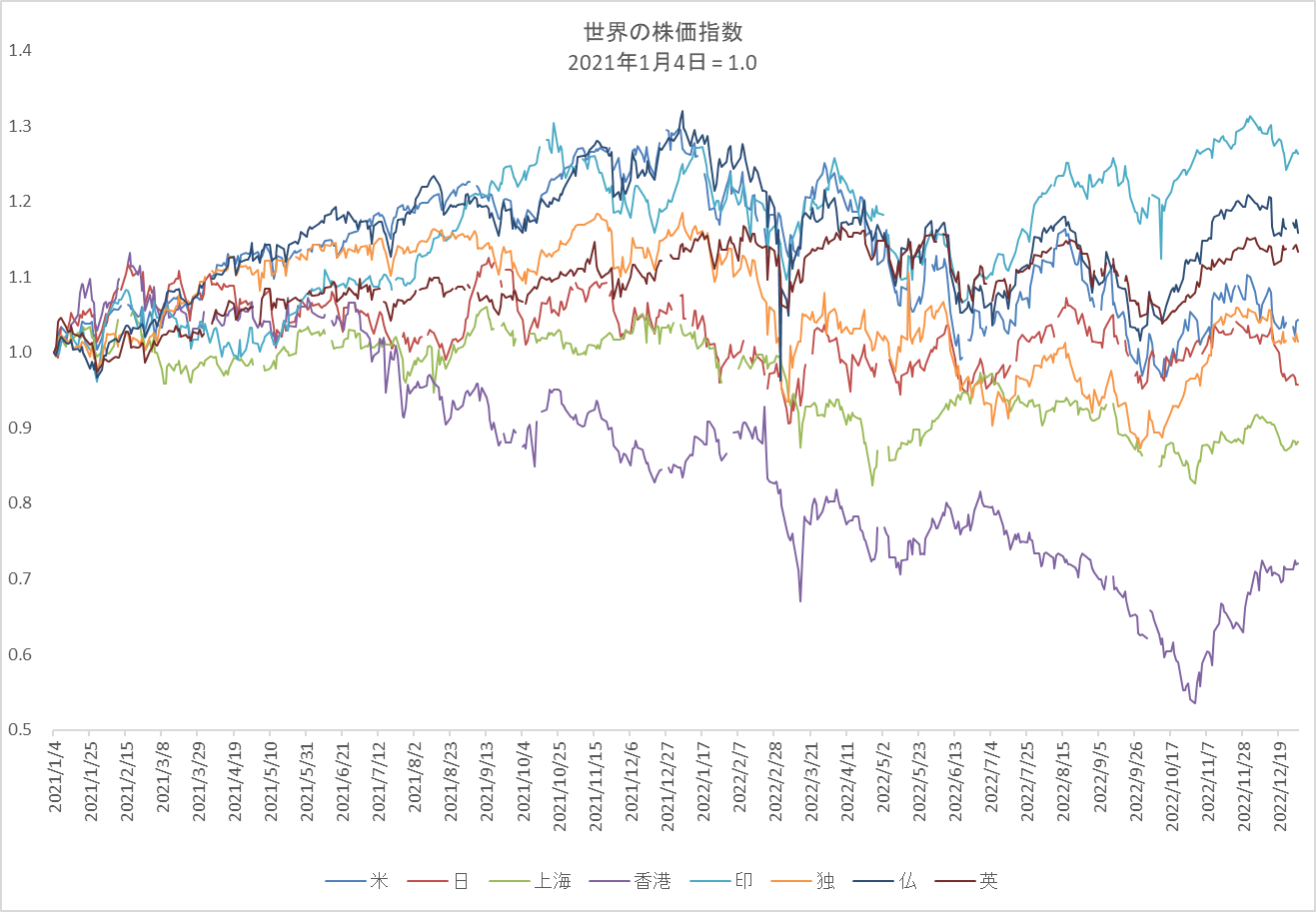
各国の主要株価指数(米 S&P500、日本 N225、上海 SSE、香港 HSI、印 BSESN、独 GDAXI、仏 FCHI、英 FTSE)の推移。
二年後の2022年12月30日の終値は、米 1.043、日本 0.957、上海 0.882、香港 0.720、印 1.263、独 1.014、仏 1.158、英 1.134。
時間経過とともにばらつきが大きくなり、インドのように大きく成長しているケースもあれば、香港や上海のようにマイナス成長になっている国もあります。八か所の証券取引所から発表された日次終値のデータの一年後と二年後のヒストグラムを比べてみると、
図2-1 図2-2
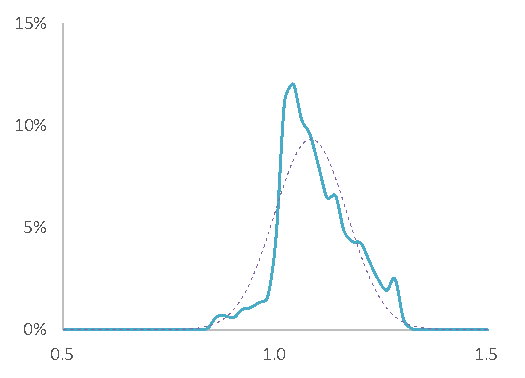

横軸が2021年1月4日の株価を $1.0$ としたときの倍率。縦軸は、その出現確率。
図2-1が一年間の分布(データ数$=2009$)、図2-2が二年間の分布(データ数$=4052$)。データ区間$=0.2$。
破線はデータから得られた平均と標準偏差で描いた正規分布。いずれも確率分布であるため実線と破線に囲まれた面積は $1.0$。
となり、ばらつきが大きくなっていることがわかります。図1と図2を重ね合わせて確認してみましょう。
図3
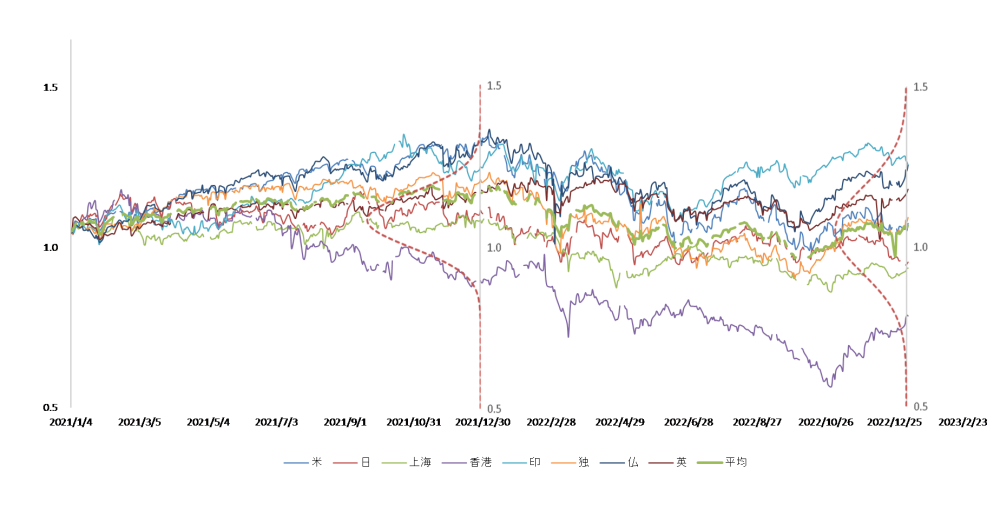
図1と図2の重ね合わせ。データの分布推移がよくわかる。
2021年の一年間と2021年から2022年の二年間の平均と標準偏差を比較すると、
表1
| 2021年 | 2021~2022年 | 増減 | |
| 平均 | 1.082 | 1.049 | -3% |
| 標準偏差 | 0.086 | 0.136 | +58% |
となっており、平均が若干のマイナスであったのに比べ、ばらつき度合いを示す標準偏差が大幅に増加しているのがわかります。
ところで図2のような「ばらつきの増加現象」を数式化することができるでしょうか。熱伝導方程式は、
$$\frac{{\partial}n}{{\partial}t}=D\frac{{{\partial}^2}n}{{\partial}x^2}\tag{1}$$
という形をしていました。この方程式を差分化して、任意の時間 $t$ 、位置 $x$ における $n$ を図式化すると、
図4
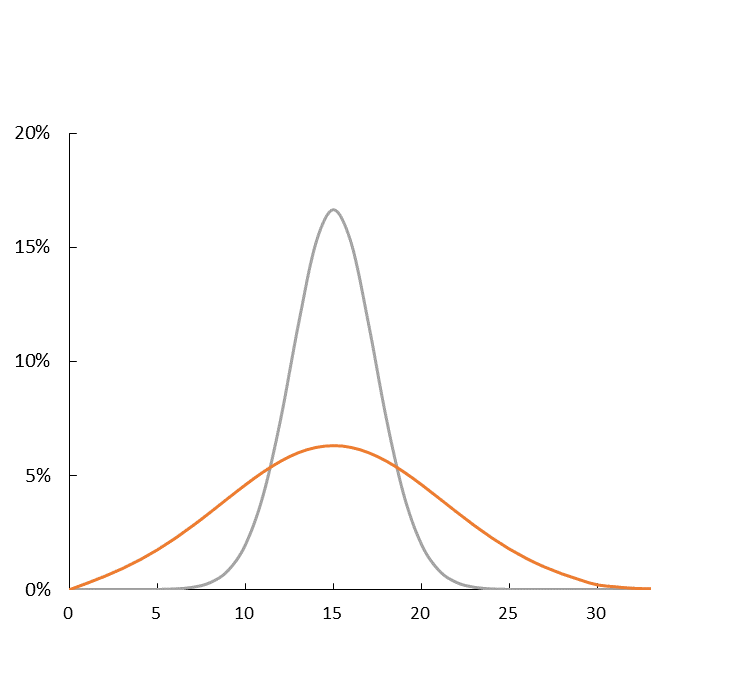
熱伝導方程式を解くと得られるベルカーブ。縦軸は出現確率、横軸は位置 $x$。いずれも面積は $1.0$。
$⊿x=1.0, ⊿t=0.01, D=1.0$。
のようになります。断熱した長い金属棒の中央に一定の熱を加えたとき、その熱が金属棒をにどのように伝わっていくかをイメージするといいでしょう。熱が平準化していく様子は株価の拡散と酷似しています。
式 (1) の $D$ は拡散係数です。この値が大きくなると山が低くなって裾野が広がります。逆に小さくなると山が高くなって裾野が狭くなります。
ところで、表2の平均に注目すると、図2-2の方がわずかに小さいです。これは、株価の確率分布曲線(以後、親しみを込めて「株価ベルカーブ」と呼びます)の頂点が少し左に移動することを意味します。当然、その逆もあり得ますので、株価ベルカーブは左右(図3では上下)どちらにも動きます。よって、方程式をより現実の動きに近づけるには、拡散しながらも左右へ移流するように式 (1) を書き換える必要があります。
式 (2) は、式 (1) の右辺に第二項として $C\frac{{\partial}n}{{\partial}x}$ を加えた形になっています。$C$ は移流係数です。この係数の値が大きいと左右への移流スピードが速くなり、小さいと遅くなります。さきほどと同様に差分化して数値計算してみると、移流係数 $C$ が負のときは右方向へ、正のときは左方向へ移動することがわかります。
図5-1 図5-2


株価ベルカーブの拡散移流。式 $(2)$ の移流係数 $C$ が負のときは右へ(図4-1)、正のときは左へ(図4-2)移流する。
⊿x=0.8, ⊿t=0.1, C=±1.0, D=1.0
理論はこれでよさそうなので、式 (2) から得られる計算解と図2-2(2021年~2022年の確率分布)を重ね合わせて、移流係数 $C$ と拡散係数 $D$ を探り出してみましょう。
図6
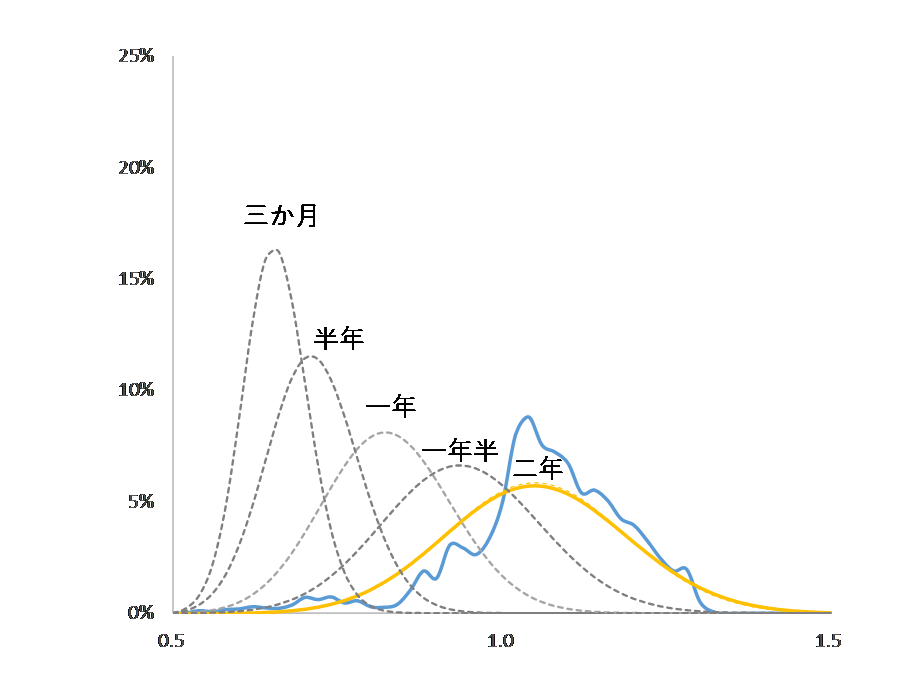
縦軸が出現確率、横軸が 位置 $x$。青色の実線が2021~2022年の分布実績。
理論分布(グレーの破線)を実績(黄色の実線)に重ね合わせることで、移流係数 $C$ と拡散係数 $D$ を探り出すことができる。
手順は以下のとおりです。
<手順1> 図5-1の横軸 $x$ を $0.5$ ~ $1.5$ の範囲に変更する。きざみ幅 ⊿x=0.02。
<手順2> 式 $(2)$ を差分化して縦を時間 $t$ と横を位置 $x$ にとったマトリクスを作成する。時間のきざみ幅は ⊿t=0.1 として、ひときざみを一日に割り当てる。二年後は $t=48(480日)$。
<手順3> <手順1>で横軸を修正した図に図2-2(実績)を重ね合わせて縦横のスケールを合わせる。
<手順4> 移流係数 $C$ と拡散係数 $D$ を微調整して、理論値(グレーの破線)を実績(黄色の実線)に重ね合わせる。
図6が<手順4>で実績と理論値がぴったり重なったときの図です。表2は一年後の実績に合わせたときと二年後の実績に合わせたときの係数の違いを示しています。
表2
| 2021年1月~12月 | 2021年1月~2022年12月 | |
| 移流係数 | 1.02 | 0.47 |
| 拡散係数 | 0.96 | 0.75 |
式 (2) は無味乾燥ですが、表2のように実際の係数値が分かってくると俄然親しみが湧いてくるのは私だけでしょうか?世界経済がどう動いてきたのか、これからどう動くのか、を定量的に解析・予測するひとつの手段として注目していきます!
おわり
記事一覧へ戻る