2022年1月22日付けのブログで、株価の「ゆらぎ」がその成長に「マイナス」の影響を与えていることを実際の試行を通して確認しました。下図は、実際にゆらぎを大きくしたときのシミュレーション結果です。
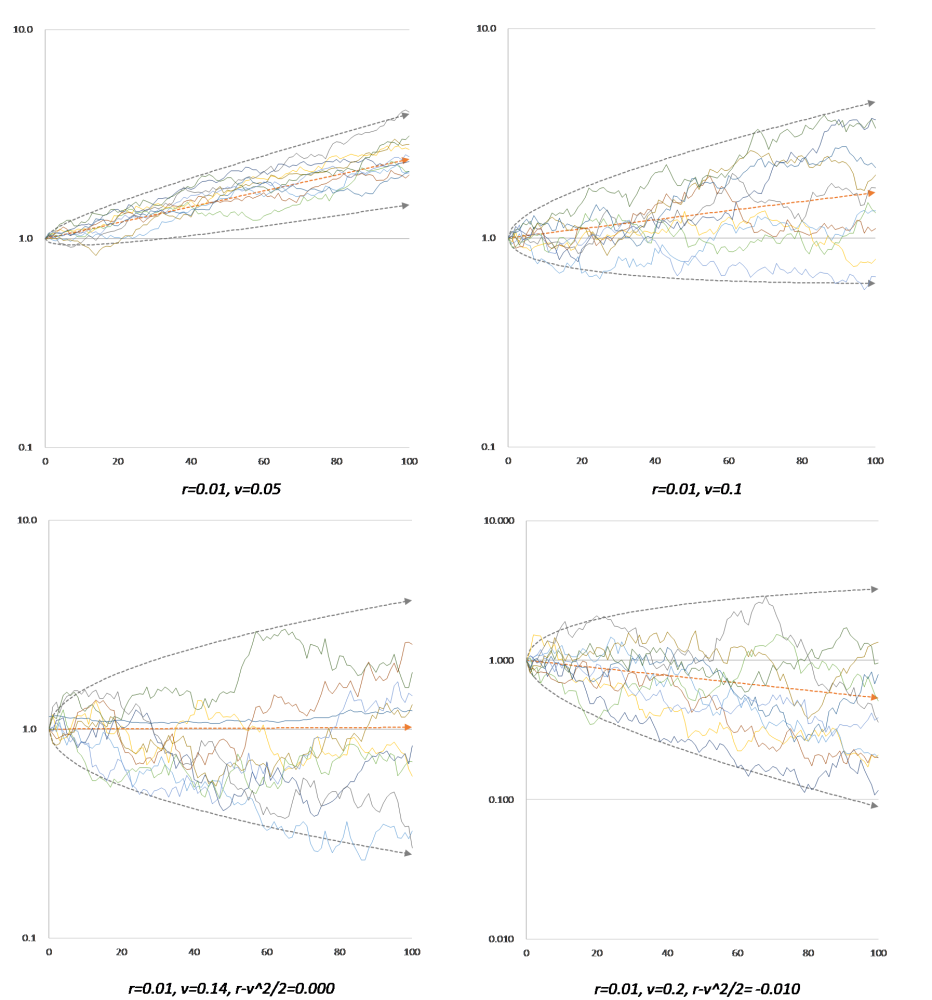
確かに、ゆらぎが大きければ大きいほどマイナス成長になってしまう確率が高くなるのがわかります。
一方、$r$ を成長係数、$v$ をゆらぎ係数、$B$ をブラウン運動(微細なランダム運動)としたとき、株価の変化率が、以下の確率微分方程式で表現できること、
$$\frac{dx}{dt}=rx+vx\frac{dB}{dt}\tag{1}$$
$x_{0}$ を初期値とすれば、ある時点 $t$ の株価 $x_{t}$ が、
$$x_{t}=x_{0}e^{(r-\frac{v^2}{2})t+vB}\tag{2}$$
であることを天下り的に紹介しました。
本日は、式 (1) からなぜ式 (2) が出てくるのか、その導出にチャレンジします。
まずは、式 (1) より、
$$dx=rxdt+vxdB\tag{3}$$
ここで、いきなりですが未知の関数 $F(x)$ をテイラー展開して極限をとります。
$$dF(x)=F'(x)dx+\frac{1}{2}F^{”}(x)(dx)^2+\cdots\tag{4}$$
式 (3) を式 (4) へ代入します。
$$dF(x)=F'(x)(rxdt+vxdB)+\frac{1}{2}F^{”}(x)(rxdt+vxdB)^2+\cdots\tag{5}$$
式 (5) に以下のルールを適用して整理すると、
$$(dB)^2\to dt\tag{6}$$
$$(dt)^2\to 0\tag{7}$$
$$dtdB\to 0\tag{8}$$
$$dF(x)=\biggl(F'(x)rx+\frac{1}{2}F^{”}(x)(vx)^2 \biggr)dt+F'(x)vxdB\tag{9}$$
ここで、またもやいきなりですが、$F(x)=\log{x}$ とすると、式 (9) は、
$$d\log{x}=\biggl(\frac{1}{x}rx-\frac{1}{2}\frac{1}{x^2}(vx)^2 \biggr)dt+\frac{1}{x}vxdB\tag{10}$$
つまり、
$$d\log{x}=(r-\frac{v^2}{2})dt+vdB\tag{11}$$
となります。左辺を $\log{x_{t}}$ と $\log{x_{0}}$ の差と捉えると、両辺から $d$ が消えて、
$$\log{x_{t}}-\log{x_{0}}=(r-\frac{v^2}{2})t+vB\tag{12}$$
となりますので、
$$\log{\frac{x_{t}}{x_{0}}}=(r-\frac{v^2}{2})t+vB\tag{13}$$
$$\frac{x_{t}}{x_{0}}=e^{(r-\frac{v^2}{2})t+vB}\tag{14}$$
$$x_{t}=x_{0}e^{(r-\frac{v^2}{2})t+vB}\tag{15}$$
式 (15) は式 (2) と同じですから、式 (1) の確率微分方程式からその解である式 (2) の導出ができたことになります。
さて、以上のプロセスの中で、ポイントは二回の「いきなり」です。一つ目は「テイラー展開」、二つ目は $F(x)=\log{x}$ と置いたところです。式 (2) のなかに $\frac{1}{2}$ と $v^2$ が入っていることから、テイラー展開が思い浮かんだり、さらにはその符号がプラスではなくマイナスであるということは、二度微分すると符号がプラスからマイナスへ変わる関数が関与しているはずだと思い当たるひとがいるのでしょう。確かに、$\log{x}$ の一階微分は $\frac{1}{x}=x^{-1}$ で、二階微分は、$-\frac{1}{x^2}=-x^{-2}$ となり符号が変わります。
そして、もうひとつポイントは、中盤に出てくる「謎のルール」
$$(dt)^2\to 0\tag{7}$$
$$dtdB\to 0\tag{8}$$
です。(7) と (8) はいいとしても、なぜ (6) の $(dB)^2$ が消えないで $dt$ に化けるのでしょうか?ここは特に注目すべきポイントです。これはブラウン運動が、平均 $0$、分散 $\sigma^2t$ の正規分布となる運動であることが理由です。つまり、$\Delta B=\pm\sigma\sqrt{\Delta t}$ なのです。よって、$(\Delta B)^2=\sigma^2t$ ですから、$\sigma=1$のとき、その極限は $(dB)^2\to dt$ となります。
テイラー展開すると、大抵は二次の項は微小につき無視されますが、 $(dB)^2$ が $dt$ に化けるのが理由で二階微分の項が生き残ります。そして、それが回りまわって $r-\frac{v^2}{2}$ として最終的な解の中にあらわれるのです。
前編でなぜ、$r-\frac{v^2}{2}$なのか?というシンプルな疑問を投げかけましたが、これでようやくその理由がわかりました。それにしても、テイラー展開や、ブラウン運動の数式化など、よくこういうことが思いつくものです。すごい!としかいいようがありません。
おわり
記事一覧へ戻る