In my blog of April 16, 2020, “Will refraining from going out hasten the containment of COVID-19 Infections? ” I used simple differential equations to derive that reducing human-to-human contact is the most effective way to decrease the number of infections. Then, did the actual number of infected people change as predicted?
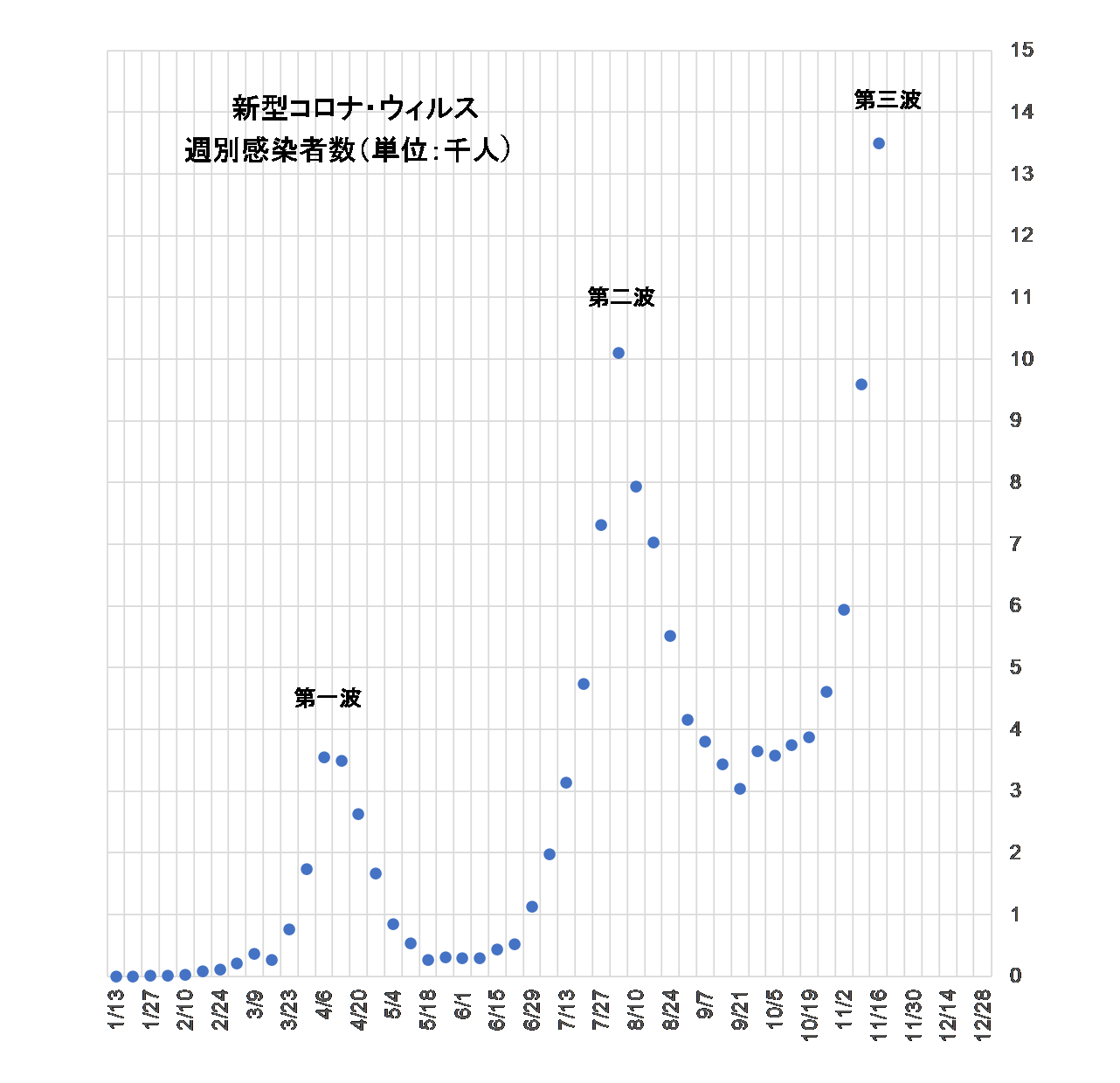
Due to the declaration of a state of emergency, the number of infected people on a weekly basis came to a halt at the end of May, but began to increase again around the end of June, reaching 10,000 by the middle of August. After that, it started to decrease, but began to stagnate when the number dropped below 4,000, and then started to increase again from October. Figure 1 is a weekly tally of the number of infected people released by the Ministry of Health, Labor and Welfare.
Figure 1
This surging phenomenon was not predicted at first. This is because, for the reasons described below, infection stops when the number of potentially infected people falls below a certain level.
People are simply divided into those who are infected with COVID-19 and those who are not infected.
The number of infected people increases with the infectivity of the virus, but once infected, immunity or death eliminates the possibility of infection.
If the coefficient for infectivity is $b$ and the coefficient for the degree of cure or death is $c$, then (1) and (2) are defined by the following differential equations.
The rate of change of $x$ for a potentially infected person :
$$frac{dx}{dt} = -bxy tag{1}$$.
Equation $(1)$ shows that $x$ decreases with contact with an infected person $y$. Since $x$ is only “people who may be infected”, for example, people who do not go out, people who have infection control measures, or people who are in an environment with such measures are excluded.
Rate of change of the number of infected people $y$: $$frac{dy}{y
$$frac{dy}{dt} = bxy – cy tag{2}$$.
Equation $(2)$ shows that contact with $x$ increases the number of infected people $y$, while cure and death decrease it. Here.
$$bxy – cy = 0$$.
then
$$x = frac{c}{b}$$.
Therefore, when $x$ reaches $frac{c}{b}$, the number of infected people $y$ will start to decrease.
However, as shown in Fig. 1, this phenomenon has already occurred twice, once as a decrease and again as an increase. If antibodies are produced after infection and the same virus is never transmitted again, it is natural to think that the second and third waves are caused by mutations in the virus itself.
However, there is another strange phenomenon here. The third wave started before the second wave had converged. There must be a cause. I hypothesize that there may be another mutant virus hiding between the second and third waves. If there was another wave in between, the number of infected people would be a composite of these three waves. The “synthetic wave” is shown by the dashed line in Figure 2.
Figure 2
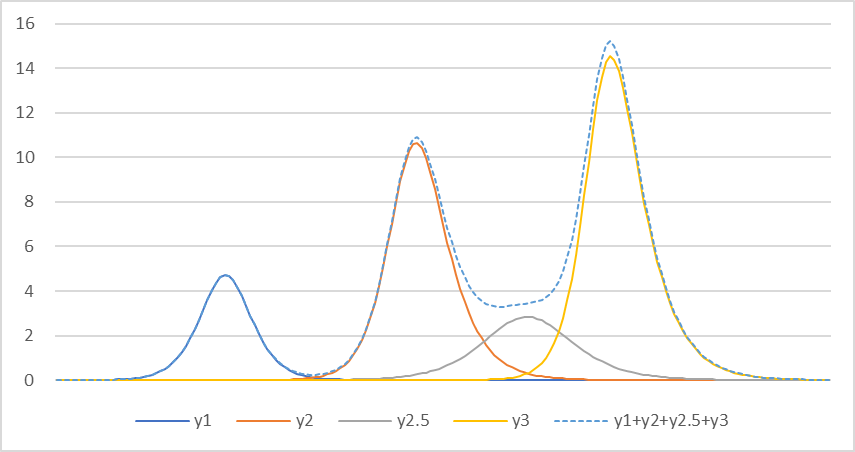
Figure 3 shows the result of fitting the synthetic wave (dashed line) to the actual data by changing the time of occurrence of the second point five waves, the infection coefficient $b$, and the cure coefficient $c$ as appropriate.
Figure 3.
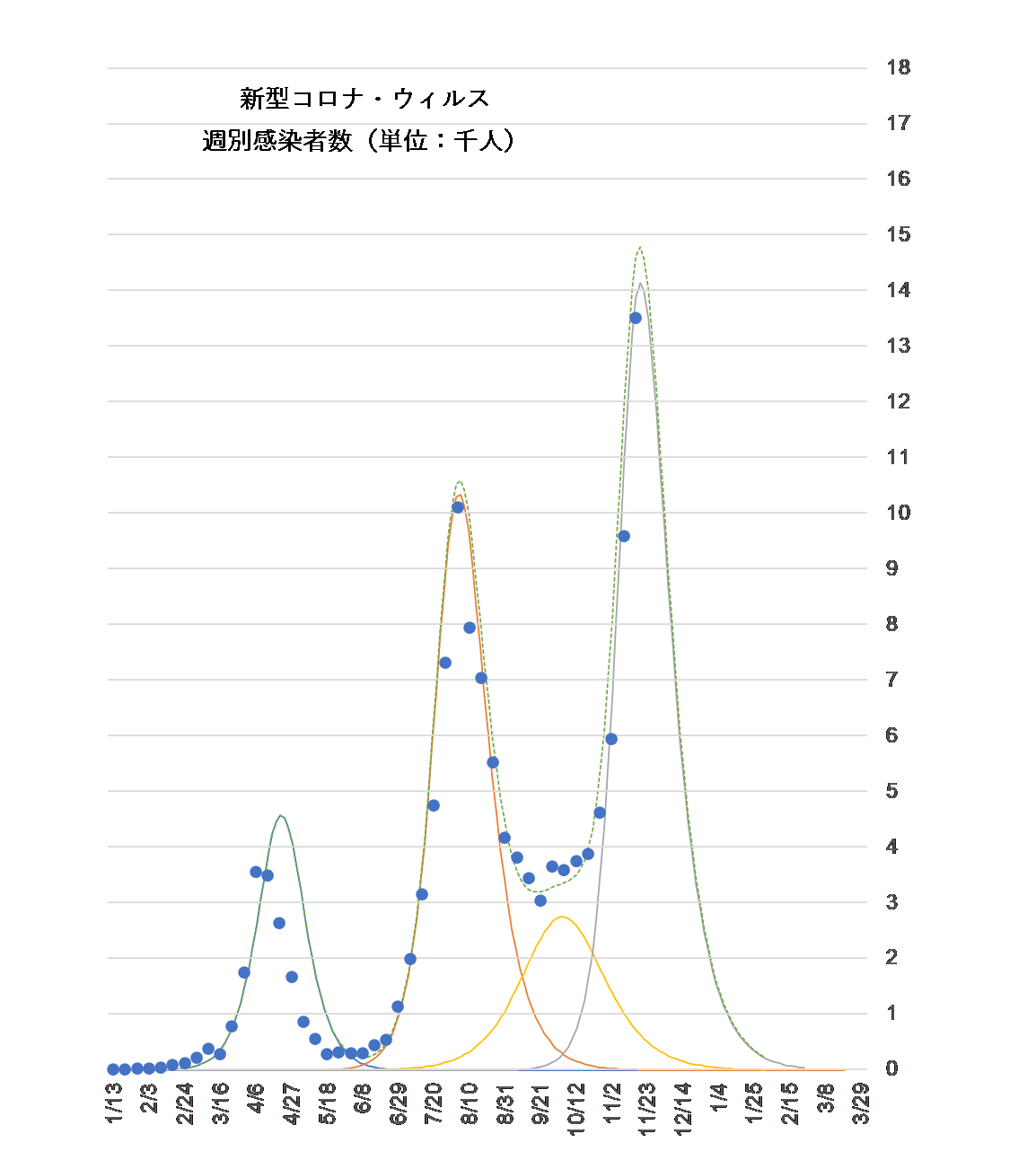
By exposing the existence of the second point five waves (solid yellow lines), the theoretical synthetic wave is well matched with the actual data.
Although we cannot deny the possibility that mutant species will continue to appear in the future, we can at least predict that the third wave (species) alone will peak at the end of November and converge around February of next year.
It has become clear that measures to prevent the spread of the disease will cause economic damage to a wide range of industries, and that there are limits to what can be done to reduce contact. Safe and effective antiviral drugs and vaccines are awaiting early commercialization and administration, but if the virus is constantly mutating, the effectiveness of medication may be limited. Mathematical theories show that infectious diseases always come to an end sooner or later, and the actual data is in line with this. We would like to deal with the situation calmly without being agitated by unnecessary fear.
The end
Back to archive