2020年4月21日付のブログでコロナショックからS&P500（米国株価指数）がいつ回復するかの予測をしました。急落前の最高値まで戻るのに一年以上かかりそうだと予測したのですが、なんと実際は半年しかかかりませんでした。コロナ禍で世界が騒然とするなか、なぜか株価だけ元気で、米国の代表的な株価指数はのきなみ史上最高値を更新しています。これはバブルであり、いつはじけてもおかしくない、というのが大方の予測です。果たして本当にそうでしょうか。

基本理論に立ち戻り、過去のデータをじっくり検証することで冷静に近未来を予測してみましょう。

＜基本理論＞

コロナ・ショックからの回復予測に使った数理論は極めてシンプルで、「株価はランダムにゆらぎながら成長する」という前提条件を以下の確率微分方程式で表現することからスタートしています。

$$\frac{dx}{dt}=rx+vx\frac{dB(t)}{dt} \tag{1}$$

  $r$ は成長係数、$v$ はゆらぎ係数、$B(t)$ はブラウン運動（ランダムウオーク）です。

式$(1)$を解くと式$(2)$になります。

$$x=x_{0}\ e^{(r-\frac{v^2}{2})+vB(t)} \tag{2}$$

係数の $r$ と $v$ は過去の動きとのフィッティングによって求めることができます（詳細は2020年4月21日付ブログを参照）。$x_{0}$ は任意の初期値です。

式 $(2)$ で、もしブラウン項の $vB(t)$ がなければ式 $(3)$ となり、株価 $x$ はこの指数増加曲線を中心として上下にゆらぎます。以下、この中心線のことを $µ$ と呼びます。

$$x=x_{0}\ e^{(r-\frac{v^2}{2})} \tag{3}$$

 

$µ$ からの離れ度合いは式 ($4$) で表せます。□が $1$の場合の指数曲線を$\pm v$、$2$の場合を $\pm 2v$、$3$ の場合は $\pm 3v$ と呼ぶことにします。

$$x=x_{0}\ e^{(r-\frac{v^2}{2}\pm □v\sqrt{t})} \tag{4}$$

 

＜過去三回の急落と回復の解析＞

コロナ・ショックのあとに何が起こるかを予測する前に、過去三回の急落とその後の動きを数理的に解析してみましょう。まずは直近のコロナ・ショックから。

図1をご覧ください。2020年2月3日の最高値から同年3月23日の底値まで、二十日間で30%の急降下です。この下落が何 $v$ に相当するのか計算してみると、マイナス $2～5v$ に相当します。地震はプレートや断層の歪が蓄積したときにそれを解消すべく発生するといわれていますが、株価も溜まったエネルギーが解放されるときに急落すると考えることができます。つまり、株価の $v$ は地震の「マグニチュード」のようなものといえます。

回復は$1v$ くらいかと予想したのですが、実際は$2～3v$ の間で推移しました。

図1

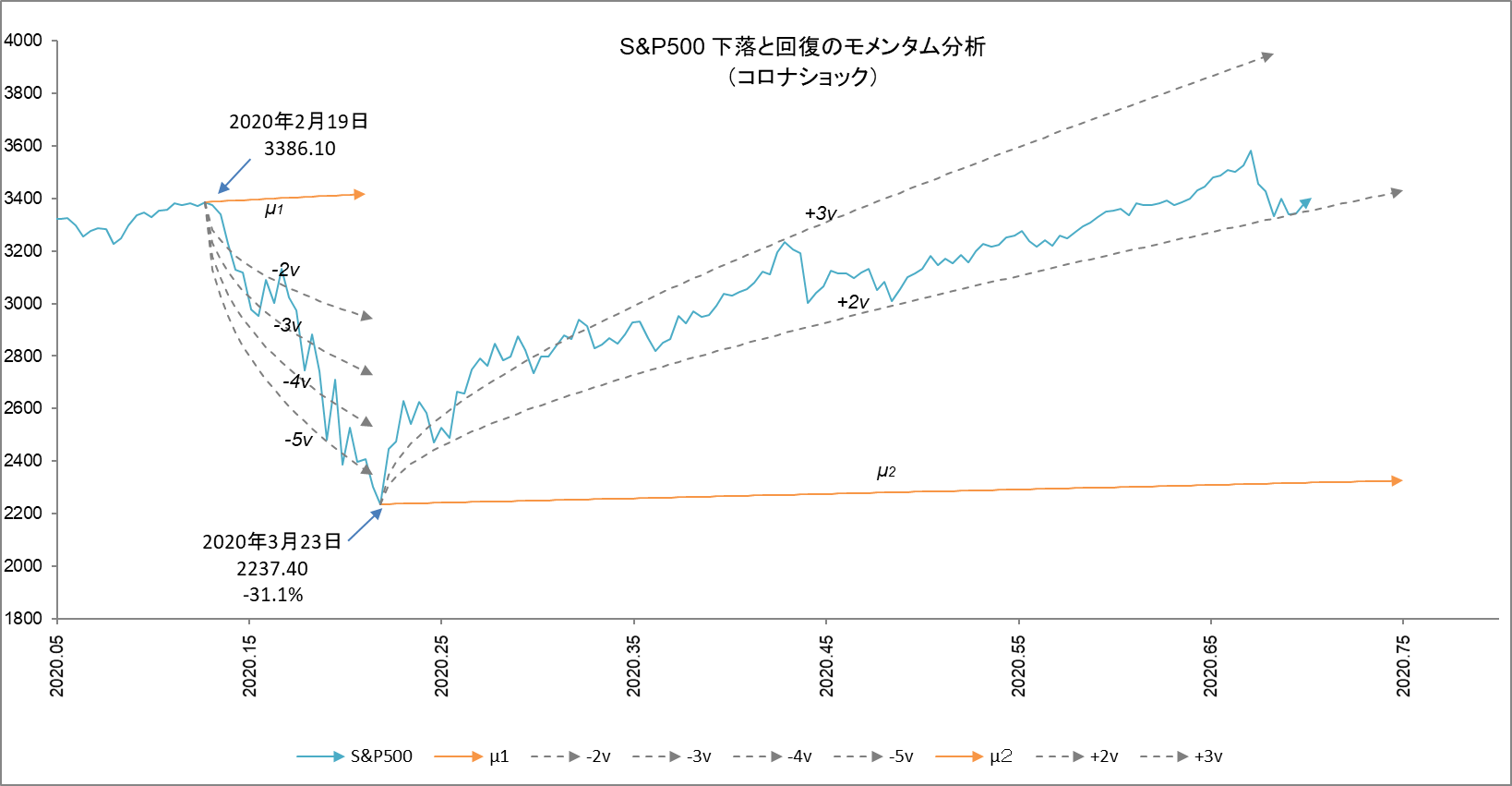
初期値x₀=3,248.92 (µ₁), x₀=2,237.40 (µ₂), 成長係数r=0.000422, ゆらぎ係数v=0.016

 

次は、「リーマン・ショック」です。発生起点を仮に2008年9月19日とし、底値を2009年3月9日とすれば、半年かけて46%の下げを記録しています。図2をご覧ください。下落の最大マグニチュードはマイナス$5v$ です。直後の回復はプラス$2～3v$ の間、その後はおおおそプラス$1v$ でした。落差が大きかったこともありショック前の最高値に戻るまで数年を要しています。

 

図2

初期値x₀=1,255.08 (µ₁), x₀=676.53 (µ₂), 成長係数r=0.000422, ゆらぎ係数v=0.016

 

「ブラック・マンデー」はどうでしょうか。図3をご覧ください。なんと、マグニチュード マイナス$11v$ の超ド級です。1987年10月13日から19日までのわずか数日間の取引で28%も暴落しました。回復は概ねプラス$1v$ です。

 

図3

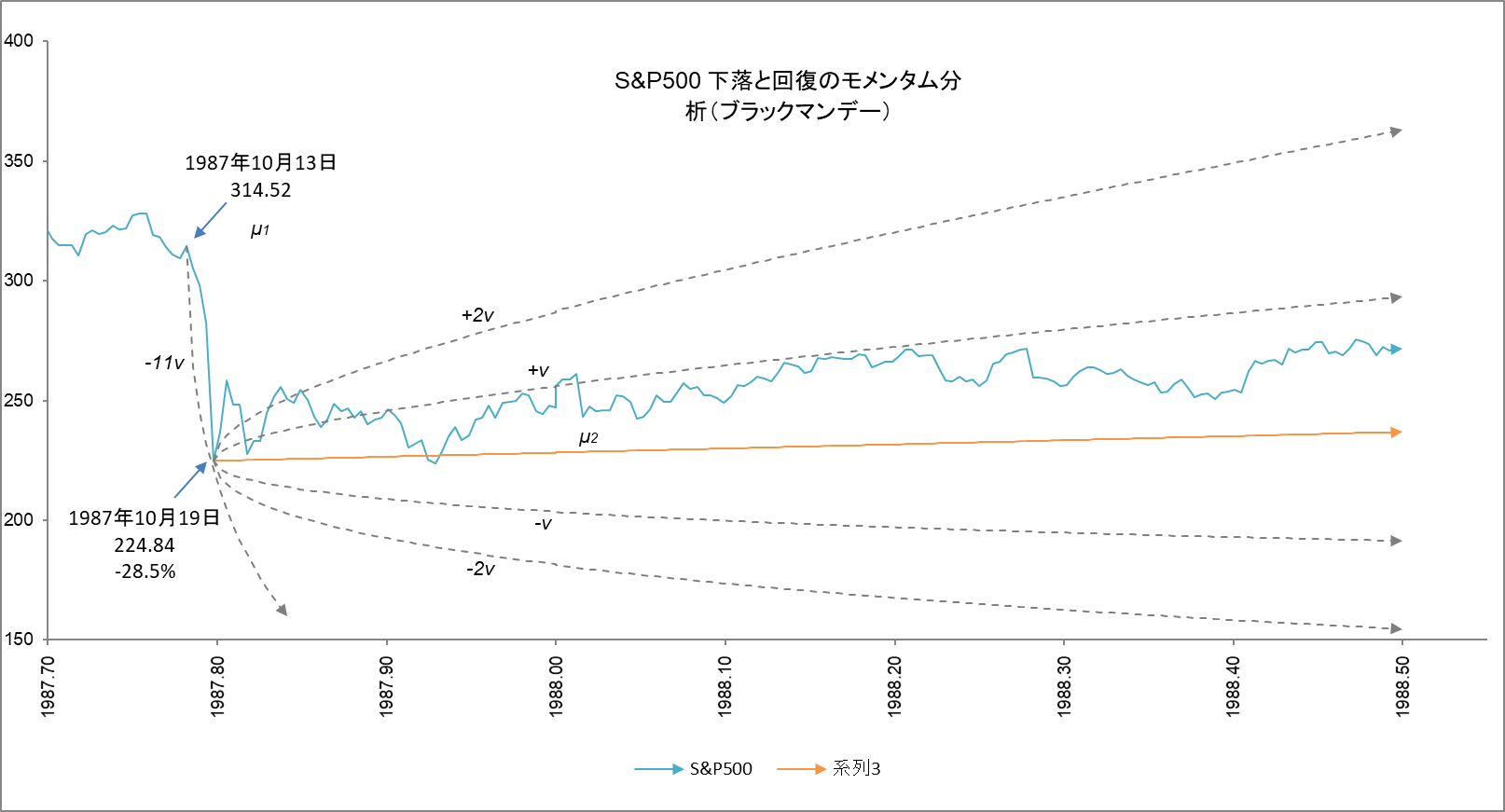
初期値x₀=314.52 (µ₁), x₀=224.84 (µ₂), 成長係数r=0.000422, ゆらぎ係数v=0.016

 

こうしてみると直近のコロナ・ショックはマグニチュード（$v$）はリーマン級、落差（下落率%）はブラック・マンデー級であったことがわかります。いずれのパターンも暴落以降、平均するとプラス$1～2v$ で回復しており、それがバブルにつながったという形跡はありません。

 

＜マクロの視点＞

では、視点をぐっと引いて、70年間の株価の動きを観察してみましょう。図1の水色の折れ線がS&P500の1950年1月3日以降の終値（日次）です。オレンジの線がµです。縦軸は対数ですので $µ$（指数曲線）は直線になります。

図5

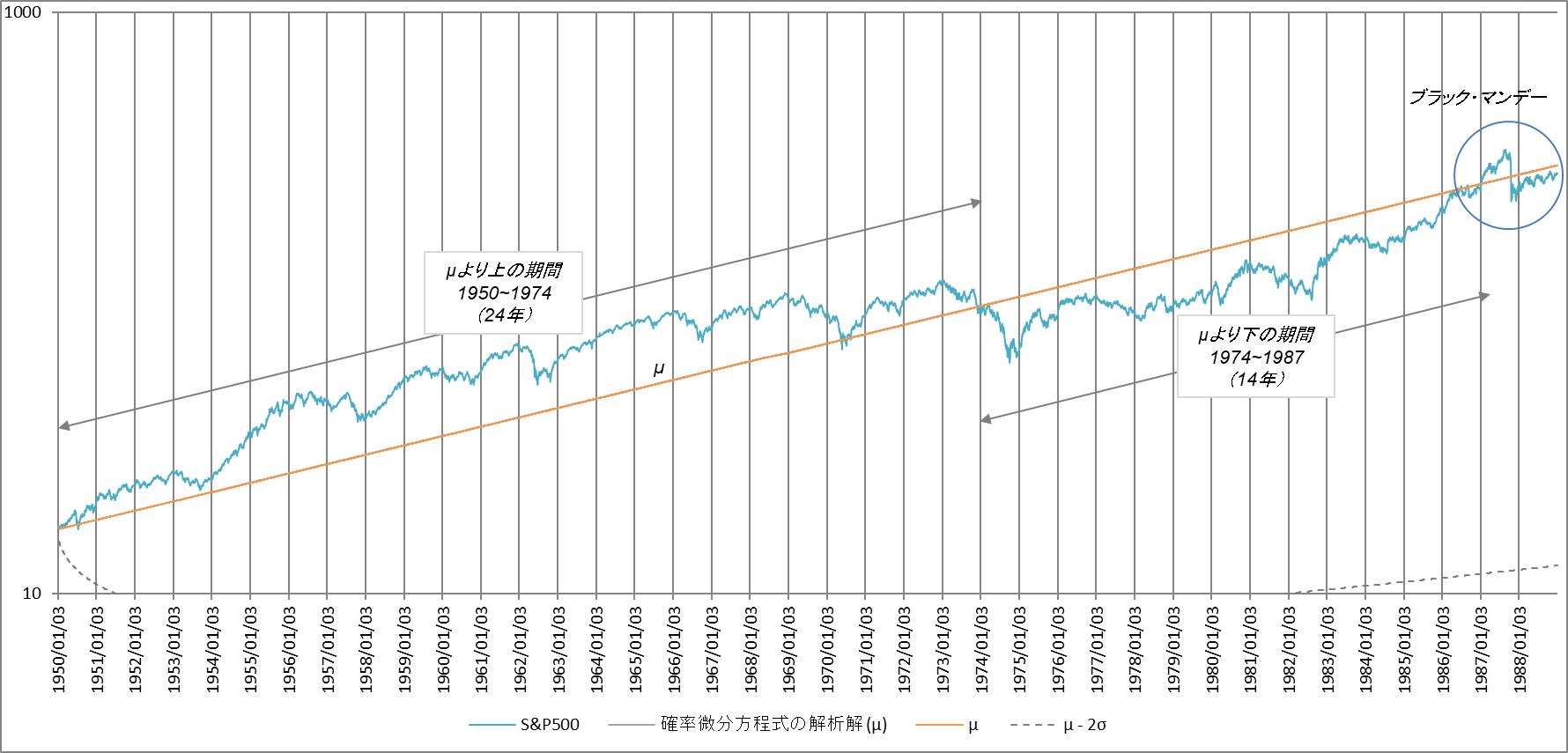
x_o=16.66, r=0.000422, v=0.016

 

図5から単純に、株価は $µ$ から離れるとまた $µ$ に戻ってくることがわかります。ざっくりですが、過去70年間で $µ$ から上にいた時期が二回（1950～1974と1995～2008）、下にいた時期が二回（1974～1987と2008～2015）、$µ$ にほぼへばりついていた時期が二回（1987～1995と2015～現在）であることもわかります。いずれも二回ずつで均等に発生していて、順番も同じです。それぞれのスパンもおおよそ均等です。

ここで、過去三回の急落がいつ発生したかに注目します。1987年のブラックマンデーはそれまで $µ$ の上と下を推移していた株価がもう一度上に突き抜けたときに発生しました。図5をご覧ください。

図5

 

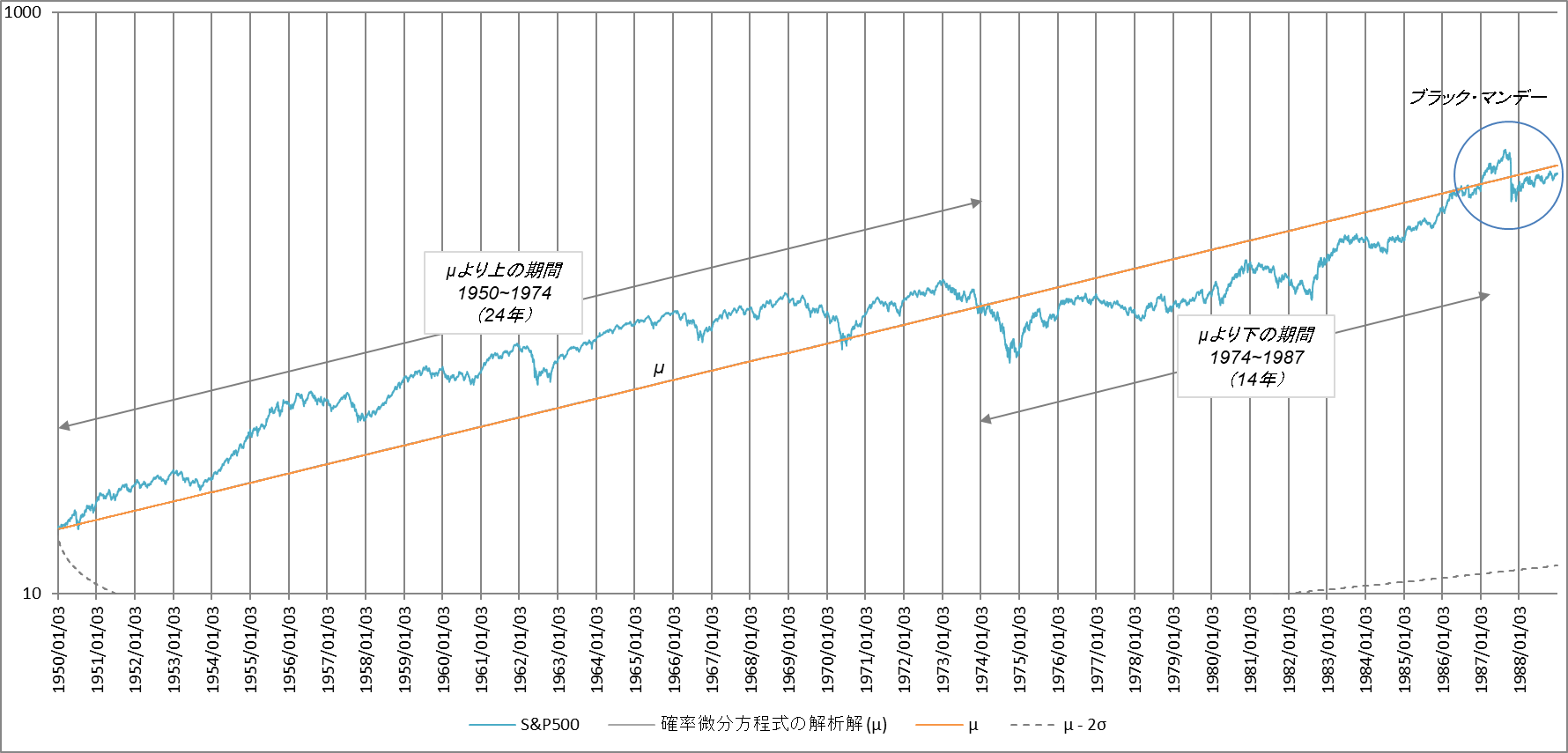
そのおかげかどうか、その後株価は $µ$ に沿って推移しましたが、1995年を境にふたたび上昇がはじまります。リーマンショックは $µ$ の上13年間に蓄積されたエネルギーを開放しました。反動で株価は一気に $µ$ の下へ移動します。その後徐々に上昇を続け、また $µ$ に戻りました。それが現在です（図6参照）。

図6

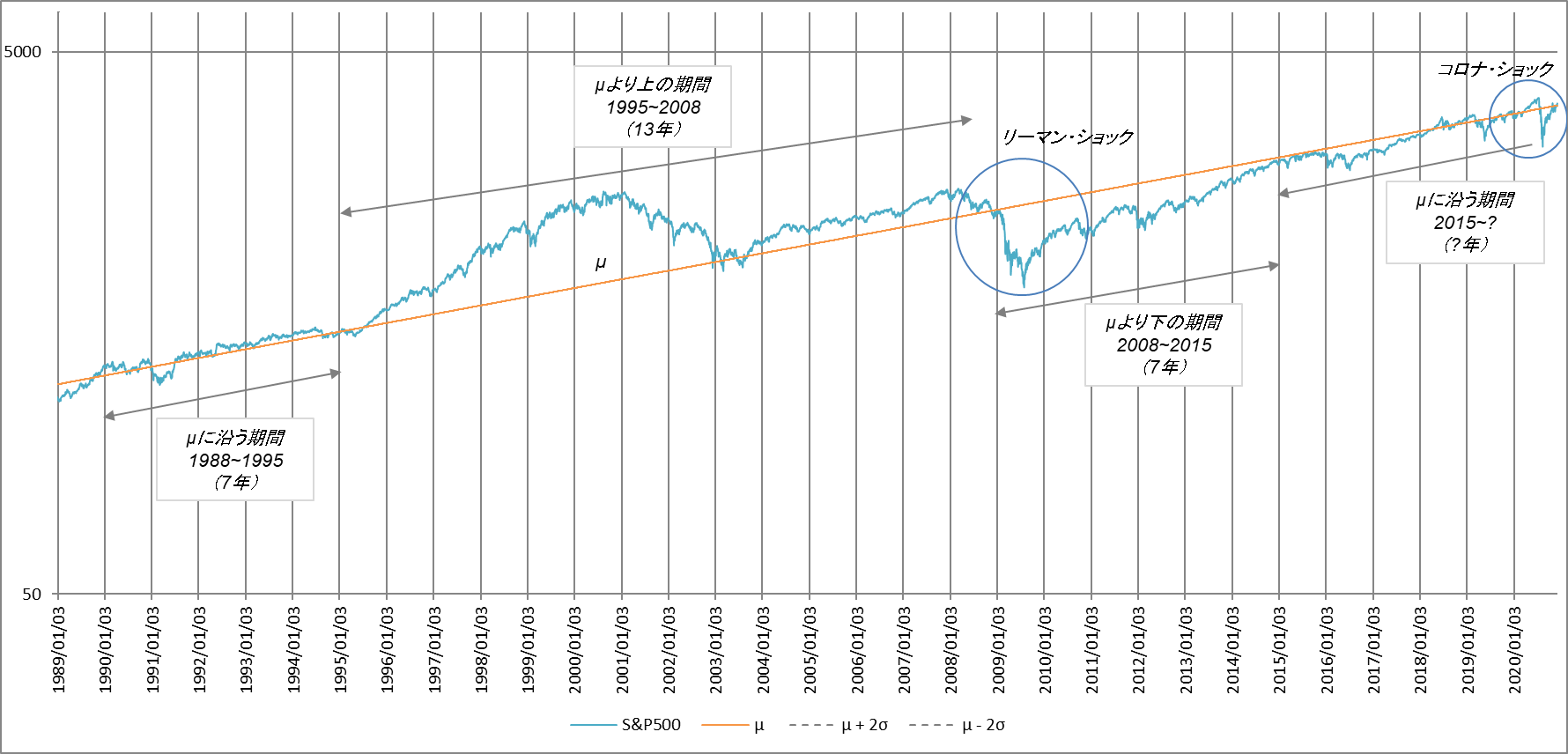
では、2020年のコロナ・ショックのあとはどうでしょうか。1950年以降の動きをマクロ的にみると、$µ$ を中心とする上下運動の順番は「$µ$ 上、$µ$ 下、$µ$ 沿」です。仮にこの順番が今後も継続するとすれば、これからは $µ$ の上へ移動します。もちろん、過去の順番が不変の法則であるという保証はありません。ただ、株価は変化率がランダムに出現する限り、$µ$ を中心に必ず上下にゆらぎます。それは、つまり、$µ$ の上にいる期間と下にいる期間がバランスするということでもあります。

株価はこれまでも史上最高値を更新してきましたし、これからも更新しますから、単純に「最高値＝バブル」という考えは誤りです。$µ$ から上下どちらの方向であっても、離れれば離れるほど、また離れる期間が長ければ長いほどµに戻ろうとするエネルギーが蓄積し、それがどこかで開放されます。それがのちに「〇○ショック」と呼ばれます。そのときにたまたま起こった社会現象が名前になったと考える方が自然です。それが証拠に1987年のブラック・マンデーには特長的な社会現象がありませんでした。

一方、株価は $µ$ から絶えず離れようとしているようにもみえます。長く $µ$ にへばりついていると $µ$ から離れようとするエネルギーが蓄積し、実際に離れます。図6 の1995年以降の動きをご覧ください。それまでの7年間、$µ$ に寄り添っていた株価は何の前触れもなく離れました。2015年から現在に至るまで、$µ$ に寄り添う期間が続いていますが、この状況はブラック・マンデーから1995年までの状態と同じです。

これらの解析から今の株価は「バブル」とはいえず、今後、急落するという大方の予想とは逆に、長期的にはむしろ上昇する可能性の方が高いという結論が導かれます。

以上

 

記事一覧へ戻る